Along with the translational and rotational motions of bodies in mechanics, oscillatory motions are also of considerable interest. Mechanical vibrations are the movements of bodies that repeat exactly (or approximately) at regular intervals. The law of motion of a body performing oscillations is specified using a certain periodic function of time x = f (t). Graphic image this function gives a visual representation of the course of the oscillatory process in time.
Examples of simple oscillatory systems are a weight on a spring or a mathematical pendulum (Fig. 2.1.1).
Mechanical vibrations, like vibrational processes of any other physical nature, can be free and forced. Free vibrations committed under the influence internal forces system, after the system has been brought out of equilibrium. Oscillations of a load on a spring or oscillations of a pendulum are free oscillations. Fluctuations occurring under the action external periodically changing forces are called forced .
The simplest type of oscillatory process is simple harmonic vibrations , which are described by the equation
|
x = x m cos (ω t + φ 0). |
Here x- displacement of the body from the equilibrium position, x m is the amplitude of oscillations, i.e., the maximum displacement from the equilibrium position, ω - cyclic or circular frequency hesitation, t- time. The quantity under the cosine sign φ = ω t+ φ 0 is called phase harmonic process. At t= 0 φ = φ 0, therefore φ 0 is called initial phase... The minimum time interval after which the repetition of body movement occurs is called period of fluctuations T... The physical quantity inverse to the oscillation period is called vibration frequency:
Oscillation frequency f shows how many oscillations are made in 1 s. Frequency unit - hertz(Hz). Oscillation frequency f is related to the cyclic frequency ω and the period of oscillations T ratios:
![]()
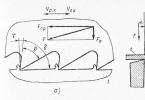
In fig. 2.1.2 shows the position of the body at regular intervals with harmonic vibrations. Such a picture can be obtained experimentally by illuminating an oscillating body with short periodic flashes of light ( stroboscopic lighting). The arrows represent the velocity vectors of the body at different times.
Rice. 2.1.3 illustrates the changes that occur on the graph of the harmonic process if either the amplitude of the oscillations changes x m, or period T(or frequency f), or the initial phase φ 0.
At oscillatory motion body along a straight line (axis OX) the velocity vector is always directed along this straight line. Speed υ = υ x body movement is determined by the expression
![]()
In mathematics, the procedure for finding the limit of the ratio at Δ t→ 0 is called the computation of the derivative of the function x (t) by time t and denoted as or as x "(t) or, finally, like. For the harmonic law of motion, the calculation of the derivative leads to the following result:
The appearance of the term + π / 2 in the argument of the cosine means a change in the initial phase. The maximum modulus values of the velocity υ = ω x m are reached at those times when the body passes through equilibrium positions ( x= 0). Acceleration is determined in the same way a = ax bodies with harmonic vibrations:
![]()
hence the acceleration a is equal to the derivative of the function υ ( t) by time t, or the second derivative of the function x (t). Calculations give:
The minus sign in this expression means that the acceleration a (t) always has the opposite sign of the displacement x (t), and, therefore, according to Newton's second law, the force that forces the body to perform harmonic oscillations is always directed towards the equilibrium position ( x = 0).
>> Harmonic vibrations
§ 22 HARMONIC VIBRATIONS
Knowing how acceleration and the coordinate of an oscillating body are related to each other, it is possible, on the basis of mathematical analysis, to find the dependence of the coordinate on time.
Acceleration is the second time derivative of the coordinate. The instantaneous speed of a point, as you know from the course of mathematics, is the time derivative of the coordinate of a point. Acceleration of a point is the derivative of its velocity with respect to time, or the second derivative of the coordinate with respect to time. Therefore, equation (3.4) can be written as follows:
where x " is the second derivative of the coordinate with respect to time. According to equation (3.11), during free oscillations, the x coordinate changes with time so that the second derivative of the coordinate with respect to time is directly proportional to the coordinate itself and opposite to it in sign.
It is known from the course of mathematics that the second derivatives of the sine and cosine by their argument are proportional to the functions themselves, taken with the opposite sign. In mathematical analysis it is proved that no other functions have this property. All this allows us to assert with good reason that the coordinate of a body performing free vibrations changes over time according to the law of sine or passine. Figure 3.6 shows the change in the coordinate of a point with time according to the cosine law.

Periodic changes in a physical quantity depending on time, occurring according to the law of sine or cosine, are called harmonic oscillations.
Amplitude of vibrations. The amplitude of harmonic vibrations is the modulus of the greatest displacement of the body from the equilibrium position.
The amplitude can have different meanings depending on how much we displace the body from the equilibrium position at the initial moment of time, or on what speed is imparted to the body. The amplitude is determined by the initial conditions, or rather by the energy imparted to the body. But the maximum values of the sine modulus and cosine modulus are equal to one. Therefore, the solution to equation (3.11) cannot be expressed simply by sine or cosine. It should be in the form of the product of the vibration amplitude x m by sine or cosine.
Solving the equation describing free vibrations. We write the solution to equation (3.11) in the following form:

and the second derivative will be:
![]()
We got equation (3.11). Consequently, function (3.12) is a solution to the original equation (3.11). The solution to this equation will also be the function
![]()

The graph of the dependence of the coordinates of the body on time according to (3.14) is a cosine wave (see Fig. 3.6).
Period and frequency of harmonic oscillations... With fluctuations, body movements are periodically repeated. Time interval T, during which the system performs one full cycle fluctuations is called the period of fluctuations.
Knowing the period, it is possible to determine the frequency of oscillations, i.e., the number of oscillations per unit of time, for example, per second. If one oscillation occurs in time T, then the number of oscillations per second
In the International System of Units (SI), the oscillation frequency is equal to one if one oscillation occurs per second. The unit of frequency is called hertz (abbreviated: Hz) in honor of the German physicist G. Hertz.
The number of oscillations in 2 s is equal to:
The value is the cyclical, or circular, vibration frequency. If in equation (3.14) time t is equal to one period, then T = 2. Thus, if at time t = 0 x = x m, then at time t = T x = x m, that is, through a period of time equal to one period, the fluctuations are repeated.
The frequency of free vibrations is found by the natural frequency of the oscillatory system 1.
Dependence of the frequency and period of free oscillations on the properties of the system. The natural frequency of vibrations of a body attached to a spring, according to equation (3.13), is:
It is the greater, the greater the spring stiffness k, and the less, the greater the body mass m. This is easy to understand: a stiff spring imparts more acceleration to the body and changes the body's speed faster. And the more massive the body, the slower it changes speed under the influence of force. The oscillation period is:
Having a set of springs of different stiffness and bodies of different masses, it is easy to be convinced by experience that formulas (3.13) and (3.18) correctly describe the nature of the dependence of U and T on k and m.
It is remarkable that the period of oscillation of the body on the spring and the period of oscillation of the pendulum at small angles of deflection do not depend on the amplitude of the oscillations.
The modulus of the proportionality coefficient between the acceleration t and the displacement x in equation (3.10), which describes the oscillations of the pendulum, is, as in equation (3.11), the square of the cyclic frequency. Consequently, the natural frequency of oscillations of a mathematical pendulum at small angles of deflection of the thread from the vertical depends on the length of the pendulum and the acceleration of gravity:

This formula was first obtained and tested experimentally by the Dutch scientist G. Huygens, a contemporary of I. Newton. It is valid only for small yarn deflection angles.
1 In what follows, for brevity, we will often refer to the cyclic frequency simply as frequency. You can distinguish the cyclic frequency from the usual frequency by designations.
The period of oscillation increases with the length of the pendulum. It does not depend on the mass of the pendulum. It is easy to test this experimentally with various pendulums. The dependence of the oscillation period on the acceleration of gravity can also be found. The smaller g, the longer the period of oscillation of the pendulum and, therefore, the slower the clock with the pendulum runs. So, a clock with a pendulum in the form of a load on a rod will lag behind in a day by almost 3 seconds if it is lifted from the basement to the upper floor of Moscow University (height 200 m). And this is only due to the decrease in the acceleration of gravity with height.
The dependence of the oscillation period of the pendulum on the value of g is used in practice. By measuring the period of the oscillation, g can be determined very accurately. Free fall acceleration varies with latitude. But even at a given latitude, it is not the same everywhere. After all, the density crust not the same everywhere. In areas with dense rocks, the acceleration g is somewhat greater. This is taken into account when searching for minerals.
Thus, iron ore has a higher density compared to ordinary rocks. Measurements of the acceleration of gravity near Kursk, carried out under the leadership of Academician A. A. Mikhailov, made it possible to clarify the location of the iron ore. They were first discovered through magnetic measurements.
Mechanical vibration properties are used in most electronic scales. The body to be weighed is placed on a platform under which a rigid spring is installed. As a result, mechanical vibrations occur, the frequency of which is measured by an appropriate sensor. The microprocessor associated with this sensor converts the vibration frequency into the mass of the weighed body, since this frequency depends on the mass.
The resulting formulas (3.18) and (3.20) for the oscillation period indicate that the period of harmonic oscillations depends on the parameters of the system (spring stiffness, thread length, etc.)
Myakishev G. Ya., Physics. Grade 11: textbook. for general education. institutions: basic and profile. levels / G. Ya. Myakishev, BV Bukhovtsev, VM Charugin; ed. V. I. Nikolaeva, N. A. Parfentieva. - 17th ed., Rev. and add. - M.: Education, 2008 .-- 399 s: ill.
A complete list of topics by class, a calendar plan according to the school curriculum in physics online, video material on physics for grade 11 download
Lesson content lesson outline support frame lesson presentation accelerative methods interactive technologies Practice tasks and exercises self-test workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photos, pictures, charts, tables, schemes humor, anecdotes, fun, comics parables, sayings, crosswords, quotes Supplements abstracts articles chips for the curious cheat sheets textbooks basic and additional vocabulary of terms others Improving textbooks and lessonsbug fixes in the tutorial updating a fragment in the textbook elements of innovation in the lesson replacing outdated knowledge with new ones For teachers only perfect lessons calendar plan for the year guidelines discussion agenda Integrated lessonsMechanical harmonic vibration- this is a rectilinear uneven motion, in which the coordinates of an oscillating body (material point) change according to the law of cosine or sine depending on time.
According to this definition, the law of coordinate change depending on time has the form:
Where wt is the value under the cosine or sine sign; w- coefficient, the physical meaning of which will be revealed below; A is the amplitude of mechanical harmonic vibrations.
Equations (4.1) are the basic kinematic equations of mechanical harmonic vibrations.
Consider the following example. Take the Ox axis (Fig. 64). From point 0 we draw a circle with radius R = A. Let point M from position 1 begin to move along a circle with a constant speed v(or with constant angular velocity w, v = wА). After some time t, the radius will rotate through the angle f: f = wt.
With such a movement along the circumference of the point M, its projection onto the x-axis M x will move along the x-axis, the coordinate of which x will be equal to x = A cos f = = A cos wt... Thus, if a material point moves along a circle of radius A, the center of which coincides with the origin, then the projection of this point onto the x-axis (and onto the y-axis) will perform harmonic mechanical vibrations.
If the quantity wt, which stands under the cosine sign, and the amplitude A are known, then x can also be determined in equation (4.1).
The quantity wt under the cosine (or sine) sign, which uniquely determines the coordinate of the oscillating point at a given amplitude, is called swing phase... For a point M moving in a circle, the value w means its angular velocity. What is the physical meaning of the quantity w for the point M x performing mechanical harmonic vibrations? The coordinates of the oscillating point M x are the same at some point in time t and (T +1) (from the definition of the period T), i.e. A cos wt = A cos w (t + T), which means that w(t + T) - wt = 2 PI(from the periodicity property of the cosine function). Hence it follows that

Therefore, for a material point performing harmonic mechanical vibrations, the value w can be interpreted as the number of vibrations for a certain cycle time equal 2L... Therefore, the value w named cyclical(or circular) frequency.
If point M begins to move not from point 1 but from point 2, then equation (4.1) will take the form:
The quantity f 0 are called initial phase.
We find the speed of the point M x as a derivative of the coordinate with respect to time:
The acceleration of a point vibrating according to a harmonic law is defined as a derivative of the speed:
From formula (4.4) it can be seen that the speed of a point performing harmonic oscillations also changes according to the cosine law. But the phase speed is ahead of the coordinate by PI / 2... Acceleration during harmonic oscillation changes according to the cosine law, but is ahead of the coordinate in phase by NS... Equation (4.5) can be written in terms of the x coordinate:
Acceleration during harmonic oscillations is proportional to the displacement with the opposite sign. We multiply the right and left sides of equation (4.5) by the mass of the oscillating material point m, we obtain the relations:
According to Newton's second law, the physical meaning of the right-hand side of expression (4.6) is the projection of the force F x, which provides harmonic mechanical motion:
The value of F x is proportional to the displacement x and is directed opposite to it. An example of such a force is the elastic force, the magnitude of which is proportional to the deformation and is directed opposite to it (Hooke's law).
The regularity of the dependence of acceleration on displacement, which follows from equation (4.6), which we considered for mechanical harmonic oscillations, can be generalized and applied when considering oscillations of another physical nature (for example, a change in the current in an oscillatory circuit, a change in charge, voltage, induction magnetic field etc.). Therefore, equation (4.8) is called the basic equation harmonic dynamics.
Consider the movement of a spring and mathematical pendulum.
Let a body of mass m be attached to the spring (Fig. 63), located horizontally and fixed at point 0, which can move along the x-axis without friction. Let the coefficient of stiffness of the spring be equal to k. Let us take the body m out of the equilibrium position with an external force and let it go. Then along the x-axis only an elastic force will act on the body, which, according to Hooke's law, will be equal to: F yпp = -kx.
The equation of motion for this body will be:

Comparing equations (4.6) and (4.9), we draw two conclusions:

From formulas (4.2) and (4.10) we derive the formula for the period of oscillation of the load on the spring:
A mathematical pendulum is a body of mass m, suspended on a long inextensible thread of negligible mass. In the equilibrium position, the gravity force and the elastic force of the thread will act on this body. These forces will balance each other.
If the thread is deflected at an angle a from the equilibrium position, then the same forces act on the body, but they no longer counterbalance each other, and the body begins to move along the arc under the action of the gravity component directed along the tangent to the arc and equal to mg sin a.
The equation of motion of the pendulum takes the form:
The minus sign on the right side means that the force F x = mg sin a is directed against the displacement. Harmonic oscillation will occur at small angles of deflection, i.e., under the condition a 2 * sin a.
Replace sin and in equation (4.12), we obtain the following equation.
The movement of the pendulum in the clock, the earthquake, alternating current v electrical circuit, the processes of radio transmission and radio reception are completely different, unrelated processes. Each of them has its own special reasons, but they are united by one sign - a sign of the generality of the nature of the change. physical quantities over time. These and many other processes of a different physical nature in many cases it turns out to be expedient to consider as one special type physical phenomena- fluctuations.
A common feature of physical phenomena called oscillations is their recurrence over time. With a different physical nature, many vibrations occur according to the same laws, which makes it possible to apply general methods for their description and analysis.
Harmonic vibrations. Of the large number of different vibrations in nature and technology, harmonic vibrations are especially common. Oscillations that occur according to the law of cosine or sine are called harmonic:
where is the value undergoing fluctuations; - time; is a constant, the meaning of which will be clarified further.
The maximum value of a quantity that changes according to a harmonic law is called the amplitude of the oscillations. The argument of the cosine or sine for harmonic oscillations is called the phase of the oscillation
The phase of the oscillation at the initial moment of time is called the initial phase. The initial phase determines the value of the quantity at the initial moment of time
The values of the sine or cosine function are repeated when the argument of the function changes to, therefore, with harmonic oscillations, the values of the quantity are repeated when the phase of the oscillation changes to. On the other hand, with a harmonic oscillation, the value should take on the same values after an interval of time called the oscillation period T. Therefore, the phase change does not occur.

through the oscillation period T. For the case when we get:

From expression (1.2) it follows that the constant in the equation of harmonic oscillations is the number of oscillations occurring in seconds. The quantity is called the cyclical frequency of oscillations. Using expression (1.2), equation (1.1) can be expressed through the frequency or period T of oscillations:
Along with the analytical way of describing harmonic oscillations, graphical methods of their presentation are widely used.
The first way is to set a graph of oscillations in a Cartesian coordinate system. The time I is plotted along the abscissa, and the value of the changing quantity is plotted along the ordinate. For harmonic oscillations, this graph is a sinusoid or cosine (Fig. 1).
The second way to represent the vibrational process is spectral. The amplitude is measured along the ordinate, and the frequency of harmonic oscillations along the abscissa. A harmonic oscillatory process with frequency and amplitude is represented in this case by a vertical segment of a straight line with a length drawn from a point with a coordinate on the abscissa axis (Fig. 2).


The third way to describe harmonic oscillations is the vector diagram method. In this method, the following, purely formal technique is used to find at any moment of time the value of a quantity varying according to a harmonic law:
![]()
We choose on the plane an arbitrarily directed coordinate axis by which we will count the value of interest to us From the origin along the axis, we draw a vector whose modulus is equal to the amplitude of the harmonic oscillation хт. If we now imagine that the vector rotates around the origin in the plane with constant angular velocity counterclockwise, then the angle a between the rotating vector and the axis at any time will be determined by the expression.
Harmonic vibrations - vibrations performed according to the laws of sine and cosine. The following figure shows a graph of the change in the coordinate of a point over time according to the law of cosine.
picture
Amplitude of vibration
The amplitude of the harmonic vibration is called greatest value displacement of the body from the equilibrium position. The amplitude can take on different values. It will depend on how much we displace the body at the initial moment of time from the equilibrium position.
The amplitude is determined by the initial conditions, that is, the energy imparted to the body at the initial moment of time. Since sine and cosine can take values in the range from -1 to 1, then the equation must have a factor Xm, which expresses the amplitude of the oscillations. Equation of motion for harmonic vibrations:
x = Xm * cos (ω0 * t).
Oscillation period
The oscillation period is the time to complete one complete oscillation. The oscillation period is denoted by the letter T. The units of the period correspond to the units of time. That is, in SI, these are seconds.
Oscillation frequency - the number of oscillations made per unit of time. The vibration frequency is denoted by the letter ν. The oscillation frequency can be expressed in terms of the oscillation period.
ν = 1 / T.
Frequency units in SI 1 / sec. This unit of measurement is called Hertz. The number of oscillations in a time of 2 * pi seconds will be equal to:
ω0 = 2 * pi * ν = 2 * pi / T.
Oscillation frequency
This value is called the cyclic vibration frequency. In some literature, the name circular frequency is found. The natural frequency of an oscillating system is the frequency of free oscillations.
The natural frequency is calculated by the formula:
The natural frequency depends on the properties of the material and the mass of the load. The greater the stiffness of the spring, the more frequency natural vibrations. The greater the mass of the load, the lower the frequency of natural vibrations.
These two conclusions are clear. The stiffer the spring, the more acceleration it will impart to the body when the system is unbalanced. The greater the mass of the body, the slower this speed of this body will change.
Free oscillation period:
T = 2 * pi / ω0 = 2 * pi * √ (m / k)
It is noteworthy that at small angles of deflection, the period of oscillation of the body on the spring and the period of oscillation of the pendulum will not depend on the amplitude of the oscillations.
Let us write down the formulas for the period and frequency of free oscillations for a mathematical pendulum.
then the period will be
T = 2 * pi * √ (l / g).
This formula will be valid only for small deflection angles. From the formula we see that the oscillation period increases with the length of the pendulum thread. The longer the length, the slower the body will oscillate.
The period of oscillations does not depend at all on the mass of the load. But it depends on the acceleration of gravity. As g decreases, the oscillation period will increase. This property is widely used in practice. For example, to measure the exact value of free acceleration.