ดังนั้นเราจึงมีพลังของทั้งสอง หากคุณนำตัวเลขมาจากบรรทัดล่างสุด คุณจะพบพลังที่คุณจะต้องยกสองขึ้นเพื่อให้ได้ตัวเลขนี้ได้อย่างง่ายดาย ตัวอย่างเช่น หากต้องการได้ 16 คุณต้องยกสองยกกำลังสี่ และเพื่อให้ได้ 64 คุณต้องยกสองยกกำลังหก ดังที่เห็นได้จากตาราง

และตอนนี้ จริงๆ แล้ว นิยามของลอการิทึม:

ฐานลอการิทึมของ x คือกำลังที่ต้องยก a เพื่อให้ได้ x

สัญลักษณ์: log a x = b โดยที่ a คือฐาน x คืออาร์กิวเมนต์ b คือค่าลอการิทึมที่แท้จริง

ตัวอย่างเช่น 2 3 = 8 ⇒ log 2 8 = 3 (ลอการิทึมฐาน 2 ของ 8 คือ 3 เพราะ 2 3 = 8) ด้วยความสำเร็จเดียวกัน บันทึก 2 64 = 6 เนื่องจาก 2 6 = 64

การดำเนินการค้นหาลอการิทึมของตัวเลขจากฐานที่กำหนดเรียกว่าลอการิทึม เรามาเพิ่มบรรทัดใหม่ให้กับตารางของเรา:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
บันทึก 2 2 = 1	บันทึก 2 4 = 2	บันทึก 2 8 = 3	บันทึก 2 16 = 4	บันทึก 2 32 = 5	บันทึก 2 64 = 6

น่าเสียดายที่ไม่ใช่ทุกลอการิทึมจะคำนวณได้ง่ายนัก ตัวอย่างเช่น ลองค้นหาบันทึก 2 5 ตัวเลข 5 ไม่ได้อยู่ในตาราง แต่ตรรกะกำหนดว่าลอการิทึมจะอยู่ที่ไหนสักแห่งในช่วงเวลา เพราะ 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

ตัวเลขดังกล่าวเรียกว่าจำนวนอตรรกยะ: ตัวเลขที่อยู่หลังจุดทศนิยมสามารถเขียนได้ไม่จำกัด และจะไม่มีวันซ้ำกัน หากลอการิทึมกลายเป็นแบบไม่ลงตัว ก็ควรปล่อยไว้อย่างนั้นดีกว่า: log 2 5, log 3 8, log 5 100

สิ่งสำคัญคือต้องเข้าใจว่าลอการิทึมคือนิพจน์ที่มีตัวแปรสองตัว (ฐานและอาร์กิวเมนต์) ในตอนแรกหลายคนสับสนว่าอะไรเป็นพื้นฐานและข้อโต้แย้งอยู่ที่ไหน เพื่อหลีกเลี่ยงความเข้าใจผิดที่น่ารำคาญ เพียงแค่ดูภาพ:

[คำบรรยายภาพ]

ก่อนหน้าเราไม่มีอะไรมากไปกว่าคำจำกัดความของลอการิทึม จดจำ: ลอการิทึมคือกำลังซึ่งจะต้องสร้างฐานเพื่อให้ได้ข้อโต้แย้ง เป็นฐานที่ยกกำลังขึ้น - ในภาพเน้นด้วยสีแดง ปรากฎว่าฐานอยู่ด้านล่างเสมอ! ฉันบอกกฎที่ยอดเยี่ยมนี้แก่นักเรียนในบทเรียนแรก - และไม่มีความสับสนเกิดขึ้น

เราเข้าใจคำจำกัดความแล้ว - สิ่งที่เหลืออยู่คือการเรียนรู้วิธีนับลอการิทึม เช่น กำจัดเครื่องหมาย "บันทึก" อันดับแรก เราสังเกตว่ามีข้อเท็จจริงสำคัญสองประการตามคำจำกัดความนี้:

1. อาร์กิวเมนต์และฐานต้องมากกว่าศูนย์เสมอ สิ่งนี้ตามมาจากคำจำกัดความของระดับด้วยเลขชี้กำลังที่เป็นตรรกยะ ซึ่งคำจำกัดความของลอการิทึมจะลดลง
2. ฐานจะต้องแตกต่างจากฐานหนึ่ง เนื่องจากระดับหนึ่งถึงระดับใดยังคงเป็นหนึ่ง ด้วยเหตุนี้ คำถามที่ว่า “คนๆ หนึ่งจะต้องเพิ่มพลังเท่าใดจึงจะได้สอง” จึงไม่มีความหมาย ไม่มีปริญญาขนาดนั้น!

ข้อจำกัดดังกล่าวเรียกว่า ช่วงของค่าที่ยอมรับได้(ODZ). ปรากฎว่า ODZ ของลอการิทึมมีลักษณะดังนี้: log a x = b ⇒ x > 0, a > 0, a ≠ 1

โปรดทราบว่าไม่มีข้อจำกัดเกี่ยวกับจำนวน b (ค่าของลอการิทึม) ตัวอย่างเช่น ลอการิทึมอาจเป็นลบ: log 2 0.5 = −1 เพราะ 0.5 = 2 −1

อย่างไรก็ตาม ตอนนี้เรากำลังพิจารณาเฉพาะนิพจน์ตัวเลข โดยไม่จำเป็นต้องทราบ VA ของลอการิทึม ผู้เขียนปัญหาได้คำนึงถึงข้อจำกัดทั้งหมดแล้ว แต่เมื่อสมการลอการิทึมและอสมการเข้ามามีบทบาท ข้อกำหนด DL จะกลายเป็นข้อบังคับ ท้ายที่สุดแล้ว พื้นฐานและการโต้แย้งอาจมีโครงสร้างที่แข็งแกร่งมากซึ่งไม่จำเป็นต้องสอดคล้องกับข้อจำกัดข้างต้น

ตอนนี้เรามาดูรูปแบบทั่วไปสำหรับการคำนวณลอการิทึม ประกอบด้วยสามขั้นตอน:

1. เขียนฐาน a และอาร์กิวเมนต์ x เป็นกำลังโดยมีฐานขั้นต่ำที่เป็นไปได้มากกว่า 1 ระหว่างทางควรกำจัดทศนิยมออกไปจะดีกว่า
2. แก้สมการของตัวแปร b: x = a b ;
3. ผลลัพธ์หมายเลข b จะเป็นคำตอบ

นั่นคือทั้งหมด! หากลอการิทึมกลายเป็นจำนวนตรรกยะ สิ่งนี้จะมองเห็นได้ในขั้นตอนแรก ข้อกำหนดที่ว่าฐานต้องมากกว่าหนึ่งมีความสำคัญมาก ซึ่งจะช่วยลดโอกาสที่จะเกิดข้อผิดพลาดและทำให้การคำนวณง่ายขึ้นอย่างมาก เช่นเดียวกับเศษส่วนทศนิยม: หากคุณแปลงเป็นเศษส่วนธรรมดาทันที จะมีข้อผิดพลาดน้อยลงมาก

มาดูกันว่าโครงร่างนี้ทำงานอย่างไรโดยใช้ตัวอย่างเฉพาะ:

งาน. คำนวณลอการิทึม: บันทึก 5 25

1. ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังของห้า: 5 = 5 1 ; 25 = 5 2 ;
2. มาสร้างและแก้สมการกัน:
   บันทึก 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. เราได้รับคำตอบ: 2.

งาน. คำนวณลอการิทึม:

[คำบรรยายภาพ]

งาน. คำนวณลอการิทึม: บันทึก 4 64

1. ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังสอง: 4 = 2 2 ; 64 = 2 6 ;
2. มาสร้างและแก้สมการกัน:
   บันทึก 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. เราได้รับคำตอบ: 3.

งาน. คำนวณลอการิทึม: log 16 1

1. ลองนึกภาพฐานและอาร์กิวเมนต์เป็นกำลังสอง: 16 = 2 4 ; 1 = 2 0 ;
2. มาสร้างและแก้สมการกัน:
   บันทึก 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. เราได้รับคำตอบ: 0.

งาน. คำนวณลอการิทึม: บันทึก 7 14

1. ลองนึกภาพฐานและข้อโต้แย้งเป็นกำลังของเจ็ด: 7 = 7 1 ; 14 ไม่สามารถแสดงเป็นกำลังของ 7 ได้ เนื่องจาก 7 1< 14 < 7 2 ;
2. จากย่อหน้าก่อนหน้า ตามมาว่าไม่นับลอการิทึม
3. คำตอบคือไม่มีการเปลี่ยนแปลง: บันทึก 7 14

หมายเหตุเล็ก ๆ เกี่ยวกับตัวอย่างสุดท้าย คุณจะแน่ใจได้อย่างไรว่าตัวเลขนั้นไม่ใช่กำลังที่แน่นอนของอีกจำนวนหนึ่ง? ง่ายมาก - แค่แยกตัวประกอบเป็นปัจจัยเฉพาะ และหากไม่สามารถรวบรวมตัวประกอบดังกล่าวเป็นกำลังที่มีเลขชี้กำลังเท่ากันได้ จำนวนเดิมก็ไม่ใช่กำลังที่แน่นอน

งาน. ค้นหาว่าตัวเลขนั้นเป็นเลขยกกำลังที่แน่นอนหรือไม่: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 - องศาที่แน่นอน เพราะ มีตัวคูณเพียงตัวเดียวเท่านั้น
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - ไม่ใช่กำลังที่แน่นอน เนื่องจากมีปัจจัยสองประการ: 3 และ 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - ระดับที่แน่นอน;
35 = 7 · 5 - ไม่ใช่กำลังที่แน่นอนอีกครั้ง
14 = 7 · 2 - ไม่ใช่ระดับที่แน่นอนอีกครั้ง

โปรดสังเกตด้วยว่าจำนวนเฉพาะนั้นมักจะเป็นกำลังที่แน่นอนของตัวมันเองเสมอ

ลอการิทึมทศนิยม

ลอการิทึมบางตัวเป็นเรื่องธรรมดามากจนมีชื่อและสัญลักษณ์พิเศษ

ลอการิทึมฐานสิบของ x คือลอการิทึมของฐาน 10 กล่าวคือ เลขยกกำลังที่ต้องยกเลข 10 เพื่อให้ได้เลข x ชื่อ: lg x.

ตัวอย่างเช่น บันทึก 10 = 1; แอลจี 100 = 2; lg 1,000 = 3 - ฯลฯ

จากนี้ไปเมื่อมีวลีเช่น “Find lg 0.01” ปรากฏในหนังสือเรียน โปรดทราบว่านี่ไม่ใช่การพิมพ์ผิด นี่คือลอการิทึมทศนิยม อย่างไรก็ตาม หากคุณไม่คุ้นเคยกับสัญกรณ์นี้ คุณสามารถเขียนใหม่ได้ตลอดเวลา:
บันทึก x = บันทึก 10 x

ทุกอย่างที่เป็นจริงสำหรับลอการิทึมธรรมดาก็เป็นจริงสำหรับลอการิทึมฐานสิบเช่นกัน

ลอการิทึมธรรมชาติ

มีลอการิทึมอื่นที่มีการกำหนดของตัวเอง ในบางแง่ มันสำคัญกว่าทศนิยมด้วยซ้ำ เรากำลังพูดถึงลอการิทึมธรรมชาติ

ลอการิทึมธรรมชาติของ x คือลอการิทึมของฐาน e เช่น ยกกำลังที่ต้องยกเลข e เพื่อให้ได้เลข x ชื่อ: ln x .

หลายคนจะถามว่า: ตัวเลข e คืออะไร? นี่เป็นจำนวนอตรรกยะ ไม่พบค่าที่แน่นอนและจดบันทึกไว้ไม่ได้ ฉันจะให้เฉพาะตัวเลขแรกเท่านั้น:
อี = 2.718281828459...

เราจะไม่ลงรายละเอียดว่าหมายเลขนี้คืออะไรและเหตุใดจึงต้องมี เพียงจำไว้ว่า e เป็นฐานของลอการิทึมธรรมชาติ:
ln x = บันทึก อี x

ดังนั้น ln e = 1; ใน อี 2 = 2; ใน อี 16 = 16 - เป็นต้น ในทางกลับกัน ln 2 เป็นจำนวนอตรรกยะ โดยทั่วไป ลอการิทึมธรรมชาติของจำนวนตรรกยะใดๆ จะเป็นจำนวนตรรกยะ ยกเว้น อย่างหนึ่ง: ln 1 = 0

สำหรับลอการิทึมธรรมชาติ กฎทั้งหมดที่เป็นจริงสำหรับลอการิทึมสามัญนั้นใช้ได้

ลอการิทึมของจำนวนที่กำหนดนั้นเรียกว่าเลขชี้กำลังซึ่งจะต้องยกจำนวนอื่นขึ้นเรียกว่า พื้นฐานลอการิทึมเพื่อให้ได้ตัวเลขนี้ ตัวอย่างเช่น ลอการิทึมฐาน 10 ของ 100 คือ 2 หรืออีกนัยหนึ่ง 10 จะต้องถูกยกกำลังสองจึงจะได้ 100 (10 2 = 100) ถ้า n– หมายเลขที่กำหนด ข– ฐานและ ล– ลอการิทึมแล้ว บี ล = น. ตัวเลข nเรียกอีกอย่างว่าแอนติลอการิทึมฐาน ขตัวเลข ล. ตัวอย่างเช่น แอนติลอการิทึมของ 2 ถึงฐาน 10 เท่ากับ 100 ซึ่งสามารถเขียนได้ในรูปแบบของบันทึกความสัมพันธ์ บีเอ็น = ลและแอนติล็อก ข = n.

คุณสมบัติพื้นฐานของลอการิทึม:

จำนวนบวกใดๆ ที่ไม่ใช่จำนวนหนึ่งสามารถใช้เป็นฐานสำหรับลอการิทึมได้ แต่น่าเสียดายที่ปรากฎว่าถ้า ขและ nเป็นจำนวนตรรกยะ ในบางกรณีซึ่งพบไม่บ่อยนักก็จะมีจำนวนตรรกยะเช่นนั้น ล, อะไร บี ล = น. อย่างไรก็ตาม สามารถกำหนดจำนวนอตรรกยะได้ ลเช่น เช่นนั้น 10 ล= 2; นี่เป็นจำนวนอตรรกยะ ลสามารถประมาณด้วยความแม่นยำที่ต้องการด้วยจำนวนตรรกยะ ปรากฎว่าในตัวอย่างนี้ ลมีค่าประมาณเท่ากับ 0.3010 และการประมาณของลอการิทึมฐาน 10 ของ 2 สามารถพบได้ในตารางลอการิทึมทศนิยมสี่หลัก ลอการิทึมฐาน 10 (หรือลอการิทึมฐาน 10) มักใช้ในการคำนวณที่เรียกว่าลอการิทึมฐาน 10 สามัญลอการิทึมและเขียนเป็น log2 = 0.3010 หรือ log2 = 0.3010 โดยละเว้นการระบุฐานของลอการิทึมอย่างชัดเจน ลอการิทึมถึงฐาน จเรียกว่าจำนวนทิพย์ประมาณ 2.71828 เป็นธรรมชาติลอการิทึม พบในงานวิเคราะห์ทางคณิตศาสตร์และการประยุกต์กับวิทยาศาสตร์ต่างๆ เป็นหลัก ลอการิทึมธรรมชาติยังเขียนได้โดยไม่ต้องระบุฐานอย่างชัดเจน แต่ใช้สัญลักษณ์พิเศษ ln เช่น ln2 = 0.6931 เนื่องจาก จ 0,6931 = 2.

การใช้ตารางลอการิทึมสามัญ

ลอการิทึมปกติของตัวเลขคือเลขยกกำลังที่ต้องยก 10 เพื่อให้ได้ตัวเลขที่กำหนด เนื่องจาก 10 0 = 1, 10 1 = 10 และ 10 2 = 100 เราจะได้ log1 = 0, log10 = 1, log100 = 2 ทันที เป็นต้น สำหรับการเพิ่มกำลังจำนวนเต็ม 10 ในทำนองเดียวกัน 10 –1 = 0.1, 10 –2 = 0.01 ดังนั้น log0.1 = –1, log0.01 = –2 เป็นต้น สำหรับจำนวนเต็มลบทั้งหมด กำลัง 10 ลอการิทึมปกติของจำนวนที่เหลือจะอยู่ระหว่างลอการิทึมของจำนวนเต็มที่ใกล้ที่สุดคือ 10 log2 ต้องอยู่ระหว่าง 0 ถึง 1, log20 ต้องอยู่ระหว่าง 1 ถึง 2 และ log0.2 ต้องอยู่ระหว่าง -1 ถึง 0 ดังนั้น ลอการิทึมจึงประกอบด้วยสองส่วน คือ จำนวนเต็มและทศนิยม ซึ่งอยู่ระหว่าง 0 ถึง 1 ส่วนจำนวนเต็มเรียกว่า ลักษณะเฉพาะลอการิทึมและถูกกำหนดโดยตัวเลขนั้นเรียกว่าส่วนเศษส่วน แมนทิสซาและหาได้จากตาราง นอกจากนี้ log20 = log(2ґ10) = log2 + log10 = (log2) + 1 ลอการิทึมของ 2 คือ 0.3010 ดังนั้น log20 = 0.3010 + 1 = 1.3010 ในทำนองเดียวกัน log0.2 = log(2о10) = log2 – log10 = (log2) – 1 = 0.3010 – 1 หลังจากลบ เราจะได้ log0.2 = – 0.6990 อย่างไรก็ตาม จะสะดวกกว่าหากแสดง log0.2 เป็น 0.3010 – 1 หรือ 9.3010 – 10 กฎทั่วไปสามารถกำหนดได้: ตัวเลขทั้งหมดที่ได้รับจากตัวเลขที่กำหนดโดยการคูณด้วยเลขยกกำลัง 10 จะมีแมนทิสซาที่เหมือนกันเท่ากับแมนทิสซาของตัวเลขที่กำหนด ตารางส่วนใหญ่แสดงแมนทิสซาของตัวเลขในช่วงตั้งแต่ 1 ถึง 10 เนื่องจากแมนทิสซาของตัวเลขอื่นๆ ทั้งหมดสามารถหาได้จากที่ให้ไว้ในตาราง

ตารางส่วนใหญ่ให้ลอการิทึมที่มีทศนิยมสี่หรือห้าตำแหน่ง แม้ว่าจะมีตารางเจ็ดหลักและตารางที่มีทศนิยมมากกว่านั้นก็ตาม วิธีที่ง่ายที่สุดในการเรียนรู้วิธีใช้ตารางดังกล่าวคือการดูตัวอย่าง ในการค้นหา log3.59 ก่อนอื่นเราสังเกตว่าหมายเลข 3.59 อยู่ระหว่าง 10 0 ถึง 10 1 ดังนั้นคุณลักษณะของมันคือ 0 เราพบหมายเลข 35 (ทางด้านซ้าย) ในตารางแล้วเลื่อนไปตามแถวไปยัง คอลัมน์ที่มีหมายเลข 9 อยู่ด้านบน ; จุดตัดของคอลัมน์นี้กับแถว 35 คือ 5551 ดังนั้น log3.59 = 0.5551 หากต้องการค้นหาแมนทิสซาของตัวเลขที่มีเลขนัยสำคัญ 4 หลัก คุณต้องใช้การประมาณค่า ในบางตาราง การประมาณค่าจะอำนวยความสะดวกตามสัดส่วนที่กำหนดในเก้าคอลัมน์สุดท้ายทางด้านขวาของแต่ละหน้าของตาราง ให้เราค้นหา log736.4; หมายเลข 736.4 อยู่ระหว่าง 10 2 ถึง 10 3 ดังนั้นลักษณะของลอการิทึมคือ 2 ในตารางเราพบแถวทางด้านซ้ายซึ่งมี 73 และคอลัมน์ 6 ที่จุดตัดของแถวนี้กับคอลัมน์นี้จะมี หมายเลข 8669 ในบรรดาส่วนเชิงเส้นเราพบคอลัมน์ 4 ที่จุดตัดของแถว 73 และคอลัมน์ 4 จะมีหมายเลข 2 เมื่อบวก 2 ถึง 8669 เราจะได้แมนทิสซา - มันเท่ากับ 8671 ดังนั้น log736.4 = 2.8671.

ลอการิทึมธรรมชาติ

ตารางและคุณสมบัติของลอการิทึมธรรมชาติมีความคล้ายคลึงกับตารางและคุณสมบัติของลอการิทึมสามัญ ความแตกต่างที่สำคัญระหว่างทั้งสองก็คือ ส่วนจำนวนเต็มของลอการิทึมธรรมชาติไม่มีนัยสำคัญในการกำหนดตำแหน่งของจุดทศนิยม ดังนั้นความแตกต่างระหว่างแมนทิสซาและคุณลักษณะจึงไม่มีบทบาทพิเศษ ลอการิทึมธรรมชาติของตัวเลข 5.432; 54.32 และ 543.2 เท่ากับ 1.6923 ตามลำดับ 3.9949 และ 6.2975 ความสัมพันธ์ระหว่างลอการิทึมเหล่านี้จะชัดเจนหากเราพิจารณาความแตกต่างระหว่างลอการิทึมเหล่านี้: log543.2 – log54.32 = 6.2975 – 3.9949 = 2.3026; ตัวเลขสุดท้ายไม่มีอะไรมากไปกว่าลอการิทึมธรรมชาติของหมายเลข 10 (เขียนดังนี้: ln10) log543.2 – log5.432 = 4.6052; เลขสุดท้ายคือ 2ln10 แต่ 543.2 = 10ґ54.32 = 10 2ґ5.432 ดังนั้นโดยลอการิทึมธรรมชาติของจำนวนที่กำหนด กคุณสามารถค้นหาลอการิทึมธรรมชาติของตัวเลขได้เท่ากับผลคูณของตัวเลขนั้น กในระดับใดก็ได้ nหมายเลข 10 ถ้าเป็น ln กบวก ln10 คูณด้วย n, เช่น. ฉัน( กґ10n) = บันทึก ก + n ln10 = ln ก + 2,3026n. ตัวอย่างเช่น ln0.005432 = ln(5.432ґ10 –3) = ln5.432 – 3ln10 = 1.6923 – (3ґ2.3026) = – 5.2155 ดังนั้น ตารางลอการิทึมธรรมชาติ เช่น ตารางลอการิทึมธรรมดา มักจะมีเฉพาะลอการิทึมของตัวเลขตั้งแต่ 1 ถึง 10 เท่านั้น ในระบบลอการิทึมธรรมชาติ เราสามารถพูดถึงแอนติลอการิทึมได้ แต่บ่อยครั้งจะพูดถึงฟังก์ชันเลขชี้กำลังหรือเลขชี้กำลัง ถ้า x= บันทึก ย, ที่ ย = อดีต, และ ยเรียกว่าเลขชี้กำลังของ x(เพื่อความสะดวกในการพิมพ์ก็มักจะเขียน ย= ประสบการณ์ x). เลขชี้กำลังมีบทบาทเป็นแอนติลอการิทึมของตัวเลข x.

การใช้ตารางลอการิทึมทศนิยมและลอการิทึมธรรมชาติ คุณสามารถสร้างตารางลอการิทึมในฐานใดก็ได้ที่ไม่ใช่ 10 และ จ. ถ้าล็อก ข = x, ที่ ขx = กและจึงบันทึก ซี บี x=บันทึก คหรือ xบันทึก คข=บันทึก ค, หรือ x=บันทึก ค/บันทึก คข=บันทึก ข. ดังนั้นการใช้สูตรผกผันนี้จากตารางลอการิทึมฐาน คคุณสามารถสร้างตารางลอการิทึมในฐานอื่นได้ ข. ตัวคูณ 1/log คขเรียกว่า โมดูลการเปลี่ยนแปลงจากฐาน คไปที่ฐาน ข. ไม่มีสิ่งใดขัดขวาง เช่น การใช้สูตรการผกผันหรือการเปลี่ยนจากระบบลอการิทึมระบบหนึ่งไปยังอีกระบบหนึ่ง การค้นหาลอการิทึมธรรมชาติจากตารางลอการิทึมสามัญ หรือการทำการเปลี่ยนแปลงแบบย้อนกลับ ตัวอย่างเช่น log105.432 = log จ 5.432/ล็อก จ 10 = 1.6923/2.3026 = 1.6923ґ0.4343 = 0.7350 จำนวน 0.4343 ที่ต้องคูณลอการิทึมธรรมชาติของจำนวนที่กำหนดเพื่อให้ได้ลอการิทึมสามัญ คือโมดูลัสของการเปลี่ยนไปใช้ระบบลอการิทึมสามัญ

ตารางพิเศษ

ลอการิทึมถูกประดิษฐ์ขึ้นแต่เดิมโดยใช้บันทึกคุณสมบัติ เกี่ยวกับ=บันทึก ก+ บันทึก ขและเข้าสู่ระบบ ก/ข=บันทึก ก-บันทึก ขเปลี่ยนผลคูณเป็นผลรวมและผลหารเป็นผลต่าง กล่าวอีกนัยหนึ่งถ้าเข้าสู่ระบบ กและเข้าสู่ระบบ ขทราบแล้วการใช้การบวกและการลบทำให้เราสามารถหาลอการิทึมของผลิตภัณฑ์และผลหารได้อย่างง่ายดาย อย่างไรก็ตามในทางดาราศาสตร์มักให้ค่าของบันทึก กและเข้าสู่ระบบ ขจำเป็นต้องค้นหาบันทึก ( ก + ข) หรือบันทึก ( ก – ข). แน่นอนว่าเราสามารถหาได้จากตารางลอการิทึมก่อน กและ ขจากนั้นทำการบวกหรือการลบที่ระบุ และค้นหาลอการิทึมที่ต้องการโดยอ้างอิงตารางอีกครั้ง แต่ขั้นตอนดังกล่าวจะต้องมีการอ้างอิงตารางสามครั้ง Z. Leonelli ในปี 1802 ตีพิมพ์ตารางที่เรียกว่า ลอการิทึมแบบเกาส์เซียน– ลอการิทึมสำหรับการบวกผลรวมและผลต่าง – ซึ่งทำให้สามารถจำกัดตัวเองให้เข้าถึงตารางได้เพียงคนเดียว

ในปี ค.ศ. 1624 I. Kepler ได้เสนอตารางลอการิทึมตามสัดส่วน เช่น ลอการิทึมของตัวเลข ก/x, ที่ไหน ก– ค่าคงที่ที่เป็นบวกจำนวนหนึ่ง ตารางเหล่านี้ใช้โดยนักดาราศาสตร์และนักเดินเรือเป็นหลัก

ลอการิทึมตามสัดส่วนที่ ก= 1 ถูกเรียก โคโลการิทึมและใช้ในการคำนวณเมื่อต้องจัดการกับผลคูณและผลหาร โคโลการิทึมของตัวเลข nเท่ากับลอการิทึมของจำนวนกลับ เหล่านั้น. โคโลญจน์ n= ล็อก1/ n= – บันทึก n. ถ้า log2 = 0.3010 แล้ว colog2 = – 0.3010 = 0.6990 – 1 ข้อดีของการใช้โคโลการิทึมคือเมื่อคำนวณค่าลอการิทึมของนิพจน์เช่น หน้า/รผลรวมสามเท่าของบันทึกทศนิยมบวก พี+ บันทึก ถาม+โคโลญจน์ รหาได้ง่ายกว่าบันทึกผลรวมและผลต่าง พี+ บันทึก ถาม-บันทึก ร.

เรื่องราว.

หลักการที่เป็นพื้นฐานของระบบลอการิทึมใดๆ เป็นที่รู้จักมาเป็นเวลานานแล้ว และสามารถย้อนกลับไปถึงคณิตศาสตร์ของชาวบาบิโลนโบราณ (ประมาณ 2,000 ปีก่อนคริสตกาล) ในสมัยนั้นมีการใช้การประมาณค่าระหว่างค่าตารางของจำนวนเต็มบวกของจำนวนเต็มเพื่อคำนวณดอกเบี้ยทบต้น ในเวลาต่อมา อาร์คิมิดีส (287–212 ปีก่อนคริสตกาล) ใช้กำลัง 108 เพื่อค้นหาขีดจำกัดบนของจำนวนเม็ดทรายที่ต้องใช้เพื่อเติมเต็มจักรวาลที่รู้จักในขณะนั้นให้สมบูรณ์ อาร์คิมิดีสดึงความสนใจไปที่คุณสมบัติของเลขชี้กำลังที่อยู่ภายใต้ประสิทธิผลของลอการิทึม: ผลคูณของกำลังสอดคล้องกับผลรวมของเลขชี้กำลัง ในช่วงปลายยุคกลางและต้นยุคสมัยใหม่ นักคณิตศาสตร์เริ่มหันมาสนใจความสัมพันธ์ระหว่างความก้าวหน้าทางเรขาคณิตและคณิตศาสตร์มากขึ้นเรื่อยๆ M. Stiefel ในเรียงความของเขา เลขคณิตจำนวนเต็ม(พ.ศ. 2087) ได้ให้ตารางกำลังบวกและลบของเลข 2 ดังนี้

สตีเฟลสังเกตว่าผลรวมของตัวเลขสองตัวในแถวแรก (แถวเลขชี้กำลัง) เท่ากับเลขชี้กำลังของสองตัวที่สอดคล้องกับผลคูณของตัวเลขสองตัวที่ตรงกันในแถวล่าง (แถวเลขชี้กำลัง) จากการเชื่อมโยงกับตารางนี้ Stiefel ได้กำหนดกฎสี่ข้อที่เทียบเท่ากับกฎสมัยใหม่สี่กฎสำหรับการดำเนินการกับเลขชี้กำลัง หรือกฎสี่ข้อสำหรับการดำเนินการกับลอการิทึม: ผลรวมในบรรทัดบนสอดคล้องกับผลคูณในบรรทัดล่าง การลบที่บรรทัดบนสอดคล้องกับการหารที่บรรทัดล่าง การคูณบนบรรทัดบนสอดคล้องกับการยกกำลังบนบรรทัดล่าง การหารที่บรรทัดบนสุดสอดคล้องกับการรูตที่บรรทัดล่างสุด

เห็นได้ชัดว่ากฎที่คล้ายกับกฎของสตีเฟลทำให้เจ. เนเปอร์แนะนำระบบลอการิทึมระบบแรกในงานของเขาอย่างเป็นทางการ คำอธิบายของตารางลอการิทึมที่น่าทึ่งตีพิมพ์ในปี 1614 แต่ความคิดของเนเปียร์กำลังยุ่งอยู่กับปัญหาการแปลงผลิตภัณฑ์เป็นจำนวนเงินนับตั้งแต่นั้นเป็นต้นมา กว่าสิบปีก่อนที่จะตีพิมพ์ผลงานของเขา เนเปียร์ได้รับข่าวจากเดนมาร์กว่าที่หอดูดาวไทโค บราเฮ ผู้ช่วยของเขามีวิธีการที่ทำให้ สามารถแปลงผลิตภัณฑ์เป็นผลรวมได้ วิธีการที่กล่าวถึงในข้อความที่เนเปียร์ได้รับนั้นขึ้นอยู่กับการใช้สูตรตรีโกณมิติเช่น

ดังนั้นตารางของเนเพอร์จึงประกอบด้วยลอการิทึมของฟังก์ชันตรีโกณมิติเป็นส่วนใหญ่ แม้ว่าแนวคิดเรื่องฐานจะไม่ได้รวมไว้อย่างชัดเจนในคำจำกัดความที่เนเปียร์เสนอ แต่บทบาทที่เทียบเท่ากับฐานของระบบลอการิทึมในระบบของเขานั้นเล่นด้วยตัวเลข (1 – 10 –7)ґ10 7 ซึ่งประมาณเท่ากับ 1/ จ.

เป็นอิสระจาก Naper และเกือบจะพร้อมกันกับเขา ระบบลอการิทึมซึ่งมีประเภทค่อนข้างคล้ายกันถูกคิดค้นและเผยแพร่โดย J. Bürgiในปราก ตีพิมพ์ในปี 1620 ตารางความก้าวหน้าทางคณิตศาสตร์และเรขาคณิต. เหล่านี้เป็นตารางแอนติลอการิทึมถึงฐาน (1 + 10 –4) ґ10 4 ซึ่งเป็นการประมาณตัวเลขที่ค่อนข้างดี จ.

ในระบบเนเปอร์ ลอการิทึมของตัวเลข 10 7 ถือเป็นศูนย์ และเมื่อตัวเลขลดลง ลอการิทึมก็เพิ่มขึ้น เมื่อจี. บริกส์ (ค.ศ. 1561–1631) ไปเยี่ยมเนเปียร์ ทั้งสองเห็นพ้องกันว่าการใช้เลข 10 เป็นฐานจะสะดวกกว่า และถือว่าลอการิทึมของ 1 เป็นศูนย์ จากนั้น เมื่อตัวเลขเพิ่มขึ้น ลอการิทึมของพวกมันก็จะเพิ่มขึ้น ดังนั้นเราจึงได้ระบบลอการิทึมทศนิยมสมัยใหม่ ซึ่งเป็นตารางที่บริกส์ตีพิมพ์ในงานของเขา เลขคณิตลอการิทึม(1620) ลอการิทึมถึงฐาน จแม้ว่าจะไม่ใช่คำที่ Naper แนะนำ แต่ก็มักเรียกว่า Naper's บริกส์เสนอคำว่า "คุณลักษณะ" และ "แมนทิสซา"

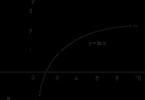
ด้วยเหตุผลทางประวัติศาสตร์ ลอการิทึมแรกใช้การประมาณตัวเลข 1/ จและ จ. ต่อมาแนวคิดเรื่องลอการิทึมธรรมชาติเริ่มมีความเกี่ยวข้องกับการศึกษาพื้นที่ใต้ไฮเปอร์โบลา เอ็กซ์ซี= 1 (รูปที่ 1) ในศตวรรษที่ 17 ปรากฏว่าพื้นที่ที่ล้อมรอบด้วยเส้นโค้งนี้ก็คือแกน xและกำหนด x= 1 และ x = ก(ในรูปที่ 1 บริเวณนี้ถูกปกคลุมไปด้วยจุดที่โดดเด่นยิ่งขึ้นและกระจัดกระจาย) ความก้าวหน้าทางคณิตศาสตร์จะเพิ่มขึ้นเมื่อ กเพิ่มขึ้นแบบทวีคูณ มันเป็นการพึ่งพาอย่างแม่นยำที่เกิดขึ้นในกฎสำหรับการดำเนินการกับเลขชี้กำลังและลอการิทึม สิ่งนี้ทำให้เกิดการเรียกลอการิทึมของ Naperian ว่า "ลอการิทึมไฮเปอร์โบลิก"

ฟังก์ชันลอการิทึม

มีครั้งหนึ่งที่ลอการิทึมถูกมองว่าเป็นวิธีการคำนวณเพียงอย่างเดียว แต่ในศตวรรษที่ 18 ต้องขอบคุณงานของออยเลอร์เป็นหลัก แนวคิดของฟังก์ชันลอการิทึมจึงถูกสร้างขึ้น กราฟของฟังก์ชันดังกล่าว ย= บันทึก xซึ่งมีลำดับเพิ่มขึ้นในการก้าวหน้าทางคณิตศาสตร์ ในขณะที่ Abscissas เพิ่มขึ้นในความก้าวหน้าทางเรขาคณิต แสดงไว้ในรูปที่ 1 2, ก. กราฟของฟังก์ชันผกผันหรือฟังก์ชันเลขชี้กำลัง y = อีเอ็กซ์ซึ่งมีการแสดงลำดับที่เพิ่มขึ้นในความก้าวหน้าทางเรขาคณิต และซึ่งมีการละเว้นเพิ่มขึ้นในความก้าวหน้าทางคณิตศาสตร์ จะถูกนำเสนอตามลำดับในรูปที่ 1 2, ข. (โค้ง ย=บันทึก xและ ย = 10xรูปร่างคล้ายกับส่วนโค้ง ย= บันทึก xและ ย = อดีต.) มีการเสนอคำจำกัดความทางเลือกของฟังก์ชันลอการิทึม เช่น

กิโลพีไอ ; และในทำนองเดียวกัน ลอการิทึมธรรมชาติของตัวเลข -1 เป็นจำนวนเชิงซ้อนในรูปแบบ (2 เค + 1)ปี่, ที่ไหน เค– จำนวนเต็ม ข้อความที่คล้ายกันนี้เป็นจริงสำหรับลอการิทึมทั่วไปหรือระบบลอการิทึมอื่นๆ นอกจากนี้ คำจำกัดความของลอการิทึมสามารถสรุปได้โดยใช้อัตลักษณ์ของออยเลอร์เพื่อรวมลอการิทึมเชิงซ้อนของจำนวนเชิงซ้อนด้วย

คำจำกัดความอื่นของฟังก์ชันลอการิทึมมีให้โดยการวิเคราะห์เชิงฟังก์ชัน ถ้า ฉ(x) – ฟังก์ชันต่อเนื่องของจำนวนจริง xโดยมีคุณสมบัติ 3 ประการดังต่อไปนี้ ฉ (1) = 0, ฉ (ข) = 1, ฉ (ยูวี) = ฉ (ยู) + ฉ (โวลต์), ที่ ฉ(x) ถูกกำหนดให้เป็นลอการิทึมของตัวเลข xขึ้นอยู่กับ ข. คำจำกัดความนี้มีข้อดีมากกว่าคำจำกัดความที่ให้ไว้ในตอนต้นของบทความนี้หลายประการ

การใช้งาน

เดิมทีลอการิทึมใช้เพื่อทำให้การคำนวณง่ายขึ้นเท่านั้น และการประยุกต์ใช้นี้ยังคงเป็นหนึ่งในรูปแบบที่สำคัญที่สุด การคำนวณผลคูณ ผลหาร กำลัง และรากไม่เพียงอำนวยความสะดวกจากตารางลอการิทึมที่เผยแพร่เท่านั้น แต่ยังรวมถึงการใช้สิ่งที่เรียกว่าด้วย กฎสไลด์ - เครื่องมือคำนวณที่มีหลักการทำงานขึ้นอยู่กับคุณสมบัติของลอการิทึม ไม้บรรทัดมีสเกลลอการิทึมเช่น ระยะห่างจากหมายเลข 1 ถึงหมายเลขใดๆ xเลือกให้เท่ากับล็อก x; การเปลี่ยนสเกลหนึ่งสัมพันธ์กับอีกสเกลหนึ่ง เป็นไปได้ที่จะพล็อตผลรวมหรือผลต่างของลอการิทึม ซึ่งทำให้สามารถอ่านผลคูณหรือผลหารของตัวเลขที่เกี่ยวข้องจากสเกลได้โดยตรง คุณยังสามารถใช้ประโยชน์จากการแสดงตัวเลขในรูปแบบลอการิทึมได้อีกด้วย กระดาษลอการิทึมสำหรับพล็อตกราฟ (กระดาษที่มีมาตราส่วนลอการิทึมพิมพ์อยู่บนแกนพิกัดทั้งสอง) ถ้าฟังก์ชันเป็นไปตามกฎกำลังของรูปแบบ y = kxnจากนั้นกราฟลอการิทึมจะมีลักษณะเป็นเส้นตรง เพราะ บันทึก ย=บันทึก เค + nบันทึก x– สมการเชิงเส้นสัมพันธ์กับบันทึก ยและเข้าสู่ระบบ x. ในทางตรงกันข้าม หากกราฟลอการิทึมของการขึ้นต่อกันของฟังก์ชันบางอย่างดูเหมือนเป็นเส้นตรง การขึ้นต่อกันนี้ก็จะเป็นแบบยกกำลัง กระดาษกึ่งบันทึก (โดยที่แกน y มีมาตราส่วนลอการิทึมและแกน x มีมาตราส่วนสม่ำเสมอ) มีประโยชน์เมื่อคุณต้องการระบุฟังก์ชันเลขชี้กำลัง สมการของแบบฟอร์ม y = กิโลไบต์ rxเกิดขึ้นเมื่อใดก็ตามที่ปริมาณ เช่น ประชากร ปริมาณของสารกัมมันตภาพรังสี หรือยอดคงเหลือของธนาคาร ลดลงหรือเพิ่มขึ้นในอัตราที่เป็นสัดส่วนกับจำนวนประชากร วัสดุกัมมันตภาพรังสี หรือเงินที่มีอยู่ในปัจจุบัน หากมีการลงจุดการพึ่งพาดังกล่าวบนกระดาษกึ่งลอการิทึม กราฟจะมีลักษณะเป็นเส้นตรง

ฟังก์ชันลอการิทึมเกิดขึ้นจากรูปแบบธรรมชาติที่หลากหลาย ดอกในช่อดอกทานตะวันเรียงกันเป็นเกลียวลอการิทึม เปลือกหอยบิดเป็นเกลียว หอยโข่งเขาแกะภูเขา และจะงอยปากนกแก้ว รูปร่างธรรมชาติทั้งหมดนี้สามารถใช้เป็นตัวอย่างของเส้นโค้งที่เรียกว่าเกลียวลอการิทึม เนื่องจากในระบบพิกัดเชิงขั้ว สมการของมันคือ r = ae bqหรือ ln ร= บันทึก ก + บาร์บีคิว. เส้นโค้งดังกล่าวอธิบายได้ด้วยจุดที่เคลื่อนที่ ระยะทางจากขั้วซึ่งมีความก้าวหน้าทางเรขาคณิตเพิ่มขึ้น และมุมที่อธิบายโดยเวกเตอร์รัศมีจะเพิ่มขึ้นในความก้าวหน้าทางคณิตศาสตร์ ความแพร่หลายของเส้นโค้งดังกล่าว และฟังก์ชันลอการิทึมนั้นแสดงให้เห็นได้ดีจากข้อเท็จจริงที่ว่ามันเกิดขึ้นในพื้นที่ห่างไกลและแตกต่างอย่างสิ้นเชิง เช่น รูปร่างของลูกเบี้ยวประหลาดและวิถีของแมลงบางชนิดที่บินเข้าหาแสง

ดังที่คุณทราบ เมื่อคูณนิพจน์ด้วยกำลัง เลขยกกำลังจะรวมกันเสมอ (a b *a c = a b+c) กฎทางคณิตศาสตร์นี้ได้รับมาจากอาร์คิมิดีส และต่อมาในศตวรรษที่ 8 นักคณิตศาสตร์วีราเซนได้สร้างตารางเลขชี้กำลังจำนวนเต็ม พวกเขาเป็นผู้ทำหน้าที่ในการค้นพบลอการิทึมเพิ่มเติม ตัวอย่างการใช้ฟังก์ชันนี้สามารถพบได้เกือบทุกที่ที่คุณต้องการลดความซับซ้อนของการคูณที่ยุ่งยากด้วยการบวกง่ายๆ หากคุณใช้เวลา 10 นาทีในการอ่านบทความนี้ เราจะอธิบายว่าลอการิทึมคืออะไรและจะทำงานร่วมกับลอการิทึมได้อย่างไร ในภาษาที่ง่ายและเข้าถึงได้

ความหมายในวิชาคณิตศาสตร์

ลอการิทึมคือนิพจน์ในรูปแบบต่อไปนี้: log a b=c นั่นคือลอการิทึมของจำนวนที่ไม่เป็นลบ (นั่นคือบวกใดๆ) “b” ไปยังฐาน “a” ถือเป็นกำลัง “c ” ซึ่งต้องยกฐาน “a” ขึ้นเพื่อให้ได้ค่า “b” ในท้ายที่สุด ลองวิเคราะห์ลอการิทึมโดยใช้ตัวอย่างสมมติว่ามีบันทึกนิพจน์ 2 8 จะหาคำตอบได้อย่างไร? ง่ายมาก คุณต้องค้นหากำลังโดยตั้งแต่ 2 ถึงกำลังที่ต้องการ คุณจะได้ 8 หลังจากคำนวณในหัวแล้ว เราก็จะได้เลข 3! และนั่นก็จริง เพราะ 2 ยกกำลัง 3 ให้คำตอบเป็น 8

ประเภทของลอการิทึม

สำหรับนักเรียนและนักเรียนหลายคนหัวข้อนี้ดูซับซ้อนและเข้าใจยาก แต่จริงๆ แล้วลอการิทึมไม่ได้น่ากลัวนัก สิ่งสำคัญคือการเข้าใจความหมายทั่วไปและจดจำคุณสมบัติและกฎบางอย่าง นิพจน์ลอการิทึมมีสามประเภทแยกกัน:

1. ลอการิทึมธรรมชาติ ln a โดยที่ฐานคือเลขออยเลอร์ (e = 2.7)
2. ทศนิยม a โดยที่ฐานคือ 10
3. ลอการิทึมของจำนวนใดๆ b ถึงฐาน a>1

แต่ละรายการได้รับการแก้ไขด้วยวิธีมาตรฐาน รวมถึงการทำให้ง่ายขึ้น การลดลง และการลดลงตามมาเป็นลอการิทึมเดียวโดยใช้ทฤษฎีบทลอการิทึม เพื่อให้ได้ค่าลอการิทึมที่ถูกต้องคุณควรจำคุณสมบัติของลอการิทึมและลำดับของการกระทำเมื่อทำการแก้ไข

กฎและข้อจำกัดบางประการ

ในทางคณิตศาสตร์ มีกฎ-ข้อจำกัดหลายประการที่ได้รับการยอมรับว่าเป็นสัจพจน์ กล่าวคือ กฎเกณฑ์เหล่านั้นไม่อยู่ภายใต้การอภิปรายและเป็นความจริง ตัวอย่างเช่น เป็นไปไม่ได้ที่จะหารตัวเลขด้วยศูนย์ และเป็นไปไม่ได้ที่จะแยกรากคู่ของจำนวนลบด้วย ลอการิทึมยังมีกฎของตัวเอง ซึ่งคุณสามารถเรียนรู้การทำงานได้อย่างง่ายดาย แม้จะมีนิพจน์ลอการิทึมที่ยาวและมีความจุมาก:

• ฐาน "a" จะต้องมากกว่าศูนย์เสมอและไม่เท่ากับ 1 มิฉะนั้นนิพจน์จะสูญเสียความหมายเนื่องจาก "1" และ "0" ในระดับใดก็ตามจะเท่ากับค่าของพวกเขาเสมอ
• ถ้า a > 0 แล้วก็ b >0 ปรากฎว่า “c” ต้องมากกว่าศูนย์ด้วย

วิธีการแก้ลอการิทึม?

ตัวอย่างเช่น มอบหมายงานให้ค้นหาคำตอบของสมการ 10 x = 100 ซึ่งง่ายมาก คุณต้องเลือกยกกำลังโดยการเพิ่มหมายเลข 10 ซึ่งเราได้ 100 แน่นอนว่านี่คือ 10 2 = 100.

ทีนี้ลองแสดงนิพจน์นี้ในรูปแบบลอการิทึม เราได้บันทึก 10 100 = 2 เมื่อแก้ลอการิทึม การกระทำทั้งหมดจะมาบรรจบกันจริงเพื่อค้นหาพลังที่จำเป็นในการเข้าสู่ฐานของลอการิทึมเพื่อให้ได้ตัวเลขที่กำหนด

ในการกำหนดค่าของระดับที่ไม่รู้จักอย่างแม่นยำ คุณต้องเรียนรู้วิธีทำงานกับตารางองศา ดูเหมือนว่านี้:

อย่างที่คุณเห็น เลขยกกำลังบางตัวสามารถเดาได้โดยสังหรณ์ใจ หากคุณมีความคิดทางเทคนิคและความรู้เกี่ยวกับตารางสูตรคูณ อย่างไรก็ตามสำหรับค่าที่มากขึ้นคุณจะต้องมีตารางกำลัง สามารถใช้งานได้แม้กับผู้ที่ไม่รู้อะไรเลยเกี่ยวกับหัวข้อทางคณิตศาสตร์ที่ซับซ้อนเลย คอลัมน์ด้านซ้ายมีตัวเลข (ฐาน a) แถวบนสุดของตัวเลขคือค่ายกกำลัง c ที่ทำให้ตัวเลข a เพิ่มขึ้น ที่ทางแยก เซลล์จะมีค่าตัวเลขที่เป็นคำตอบ (ac =b) ตัวอย่างเช่น สมมติว่าเซลล์แรกสุดที่มีหมายเลข 10 แล้วยกกำลังสอง เราจะได้ค่า 100 ซึ่งระบุไว้ที่จุดตัดของทั้งสองเซลล์ของเรา ทุกอย่างเรียบง่ายจนแม้แต่นักมนุษยนิยมที่แท้จริงที่สุดก็ยังเข้าใจ!

สมการและอสมการ

ปรากฎว่าภายใต้เงื่อนไขบางประการ เลขชี้กำลังคือลอการิทึม ดังนั้น นิพจน์ตัวเลขทางคณิตศาสตร์ใดๆ จึงสามารถเขียนเป็นความเท่าเทียมกันของลอการิทึมได้ ตัวอย่างเช่น 3 4 =81 สามารถเขียนเป็นลอการิทึมฐาน 3 ของ 81 เท่ากับสี่ (บันทึก 3 81 = 4) สำหรับกำลังลบ กฎจะเหมือนกัน: 2 -5 = 1/32 เราเขียนมันเป็นลอการิทึม เราจะได้บันทึก 2 (1/32) = -5 ส่วนที่น่าสนใจที่สุดส่วนหนึ่งของคณิตศาสตร์คือหัวข้อ "ลอการิทึม" เราจะดูตัวอย่างและคำตอบของสมการด้านล่างทันทีหลังจากศึกษาคุณสมบัติของพวกมัน ตอนนี้เรามาดูกันว่าอสมการมีลักษณะอย่างไรและจะแยกแยะพวกมันออกจากสมการได้อย่างไร

ได้รับนิพจน์ต่อไปนี้: log 2 (x-1) > 3 - เป็นอสมการลอการิทึมเนื่องจากค่าที่ไม่รู้จัก "x" อยู่ภายใต้เครื่องหมายลอการิทึม และในนิพจน์จะมีการเปรียบเทียบปริมาณสองปริมาณ: ลอการิทึมของจำนวนที่ต้องการถึงฐานสองมากกว่าจำนวนสาม

ความแตกต่างที่สำคัญที่สุดระหว่างสมการลอการิทึมและอสมการคือสมการที่มีลอการิทึม (เช่นลอการิทึม 2 x = √9) แสดงถึงค่าตัวเลขเฉพาะหนึ่งค่าขึ้นไปในคำตอบในขณะที่แก้อสมการทั้งช่วงที่ยอมรับได้ ค่าและจุดถูกกำหนดโดยทำลายฟังก์ชันนี้ ด้วยเหตุนี้ คำตอบจึงไม่ใช่ชุดตัวเลขธรรมดาๆ ดังเช่นในคำตอบของสมการ แต่เป็นชุดต่อเนื่องหรือชุดตัวเลข

ทฤษฎีบทพื้นฐานเกี่ยวกับลอการิทึม

เมื่อแก้ไขงานดั้งเดิมในการค้นหาค่าลอการิทึมอาจไม่ทราบคุณสมบัติของมัน อย่างไรก็ตาม เมื่อพูดถึงสมการลอการิทึมหรืออสมการ ก่อนอื่น จำเป็นต้องเข้าใจอย่างชัดเจนและนำไปใช้ในทางปฏิบัติเกี่ยวกับคุณสมบัติพื้นฐานทั้งหมดของลอการิทึม เราจะดูตัวอย่างสมการในภายหลัง ก่อนอื่นมาดูรายละเอียดคุณสมบัติแต่ละอย่างกันก่อน

1. ข้อมูลประจำตัวหลักมีลักษณะดังนี้: a logaB =B ใช้เฉพาะเมื่อ a มากกว่า 0 ไม่เท่ากับ 1 และ B มากกว่าศูนย์
2. ลอการิทึมของผลิตภัณฑ์สามารถแสดงได้ในสูตรต่อไปนี้: log d (s 1 * s 2) = log d s 1 + log d s 2 ในกรณีนี้เงื่อนไขบังคับคือ: d, s 1 และ s 2 > 0; ก≠1. คุณสามารถพิสูจน์สูตรลอการิทึมนี้พร้อมตัวอย่างและวิธีแก้ได้ ให้บันทึก a s 1 = f 1 และบันทึก a s 2 = f 2 จากนั้น a f1 = s 1, a f2 = s 2 เราจะได้ว่า s 1 * s 2 = a f1 *a f2 = a f1+f2 (คุณสมบัติของ องศา ) จากนั้นตามคำจำกัดความ: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2 ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์
3. ลอการิทึมของผลหารมีลักษณะดังนี้: log a (s 1/ s 2) = log a s 1 - log a s 2
4. ทฤษฎีบทในรูปแบบของสูตรจะอยู่ในรูปแบบต่อไปนี้: log a q b n = n/q log a b

สูตรนี้เรียกว่า “คุณสมบัติของระดับลอการิทึม” มันคล้ายกับคุณสมบัติขององศาธรรมดา และไม่น่าแปลกใจเลย เพราะคณิตศาสตร์ทั้งหมดมีพื้นฐานมาจากสมมุติฐานตามธรรมชาติ มาดูหลักฐานกัน

ให้บันทึก a b = t จะได้ว่า t =b ถ้าเรายกกำลังทั้งสองส่วน m: a tn = bn ;

แต่เนื่องจาก tn = (a q) nt/q = bn ดังนั้น ให้บันทึก a q bn = (n*t)/t จากนั้นให้บันทึก a q bn = n/q บันทึก a b ทฤษฎีบทได้รับการพิสูจน์แล้ว

ตัวอย่างปัญหาและความไม่เท่าเทียมกัน

ประเภทปัญหาที่พบบ่อยที่สุดในลอการิทึมคือตัวอย่างของสมการและอสมการ มีอยู่ในหนังสือโจทย์ปัญหาเกือบทั้งหมด และยังเป็นส่วนบังคับของการสอบคณิตศาสตร์ด้วย หากต้องการเข้ามหาวิทยาลัยหรือสอบเข้าวิชาคณิตศาสตร์ คุณจำเป็นต้องรู้วิธีการแก้ปัญหาดังกล่าวอย่างถูกต้อง

น่าเสียดายที่ไม่มีแผนหรือแผนงานเดียวในการแก้ไขและกำหนดค่าลอการิทึมที่ไม่ทราบ แต่กฎบางอย่างสามารถนำไปใช้กับอสมการทางคณิตศาสตร์หรือสมการลอการิทึมแต่ละรายการได้ ก่อนอื่น คุณควรค้นหาว่านิพจน์นั้นสามารถทำให้ง่ายขึ้นหรือลดลงเป็นรูปแบบทั่วไปได้หรือไม่ คุณสามารถลดความซับซ้อนของนิพจน์ลอการิทึมแบบยาวได้หากคุณใช้คุณสมบัติอย่างถูกต้อง มาทำความรู้จักกับพวกเขาได้อย่างรวดเร็ว

เมื่อแก้สมการลอการิทึม เราต้องพิจารณาว่าเรามีลอการิทึมประเภทใด: นิพจน์ตัวอย่างอาจมีลอการิทึมธรรมชาติหรือทศนิยม

นี่คือตัวอย่าง ln100, ln1026 วิธีแก้ปัญหาขึ้นอยู่กับข้อเท็จจริงที่ว่าพวกเขาจำเป็นต้องกำหนดกำลังที่ฐาน 10 จะเท่ากับ 100 และ 1,026 ตามลำดับ ในการแก้ลอการิทึมธรรมชาติ คุณต้องใช้อัตลักษณ์ลอการิทึมหรือคุณสมบัติของพวกมัน ลองดูตัวอย่างการแก้ปัญหาลอการิทึมประเภทต่างๆ

วิธีใช้สูตรลอการิทึม: พร้อมตัวอย่างและวิธีแก้ไข

ลองมาดูตัวอย่างการใช้ทฤษฎีบทพื้นฐานเกี่ยวกับลอการิทึมกัน

1. คุณสมบัติของลอการิทึมของผลิตภัณฑ์สามารถนำไปใช้ในงานที่จำเป็นต้องแยกค่า b จำนวนมากให้เป็นปัจจัยที่ง่ายกว่า เช่น log 2 4 + log 2 128 = log 2 (4*128) = log 2 512 คำตอบคือ 9
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - อย่างที่คุณเห็น การใช้คุณสมบัติที่สี่ของกำลังลอการิทึม เราจัดการเพื่อแก้นิพจน์ที่ดูเหมือนซับซ้อนและแก้ไขไม่ได้ คุณเพียงแค่ต้องแยกตัวประกอบฐานแล้วนำค่าเลขชี้กำลังออกจากเครื่องหมายของลอการิทึม

งานที่ได้รับมอบหมายจากการสอบ Unified State

ลอการิทึมมักพบในการสอบเข้า โดยเฉพาะปัญหาลอการิทึมหลายอย่างในการสอบ Unified State (การสอบของรัฐสำหรับผู้สำเร็จการศึกษาในโรงเรียนทุกคน) โดยทั่วไปแล้ว งานเหล่านี้ไม่เพียงมีอยู่ในส่วน A (ส่วนทดสอบที่ง่ายที่สุดของการสอบ) แต่ยังอยู่ในส่วน C ด้วย (งานที่ซับซ้อนและมีขนาดใหญ่ที่สุด) การสอบต้องใช้ความรู้ที่ถูกต้องและครบถ้วนในหัวข้อ “ลอการิทึมธรรมชาติ”

ตัวอย่างและวิธีแก้ปัญหานำมาจากการสอบ Unified State เวอร์ชันอย่างเป็นทางการ มาดูกันว่างานดังกล่าวจะแก้ไขอย่างไร

ให้บันทึก 2 (2x-1) = 4 วิธีแก้ไข:
ลองเขียนนิพจน์ใหม่ โดยลดความซับซ้อนของลอการิทึมเล็กๆ น้อยๆ 2 (2x-1) = 2 2 โดยนิยามของลอการิทึม เราจะได้ 2x-1 = 2 4 ดังนั้น 2x = 17; x = 8.5

• วิธีที่ดีที่สุดคือลดลอการิทึมทั้งหมดให้เป็นฐานเดียวกันเพื่อไม่ให้โจทย์ยุ่งยากและสับสน
• นิพจน์ทั้งหมดภายใต้เครื่องหมายลอการิทึมจะแสดงเป็นค่าบวก ดังนั้น เมื่อเลขชี้กำลังของนิพจน์ที่อยู่ใต้เครื่องหมายลอการิทึมและเมื่อฐานถูกนำออกมาเป็นตัวคูณ นิพจน์ที่เหลืออยู่ภายใต้ลอการิทึมจะต้องเป็นค่าบวก

การรักษาความเป็นส่วนตัวของคุณเป็นสิ่งสำคัญสำหรับเรา ด้วยเหตุนี้ เราจึงได้พัฒนานโยบายความเป็นส่วนตัวที่อธิบายถึงวิธีที่เราใช้และจัดเก็บข้อมูลของคุณ โปรดตรวจสอบหลักปฏิบัติด้านความเป็นส่วนตัวของเราและแจ้งให้เราทราบหากคุณมีคำถามใดๆ

การรวบรวมและการใช้ข้อมูลส่วนบุคคล

ข้อมูลส่วนบุคคลหมายถึงข้อมูลที่สามารถใช้เพื่อระบุหรือติดต่อบุคคลใดบุคคลหนึ่งโดยเฉพาะ

คุณอาจถูกขอให้ให้ข้อมูลส่วนบุคคลของคุณได้ตลอดเวลาเมื่อคุณติดต่อเรา

ด้านล่างนี้คือตัวอย่างบางส่วนของประเภทของข้อมูลส่วนบุคคลที่เราอาจรวบรวมและวิธีที่เราอาจใช้ข้อมูลดังกล่าว

เราเก็บรวบรวมข้อมูลส่วนบุคคลอะไรบ้าง:

• เมื่อคุณส่งใบสมัครบนเว็บไซต์ เราอาจรวบรวมข้อมูลต่าง ๆ รวมถึงชื่อ หมายเลขโทรศัพท์ ที่อยู่อีเมลของคุณ ฯลฯ

เราใช้ข้อมูลส่วนบุคคลของคุณอย่างไร:

• ข้อมูลส่วนบุคคลที่เรารวบรวมช่วยให้เราสามารถติดต่อคุณเพื่อรับข้อเสนอ โปรโมชั่น และกิจกรรมอื่น ๆ และกิจกรรมที่กำลังจะเกิดขึ้น
• ในบางครั้ง เราอาจใช้ข้อมูลส่วนบุคคลของคุณเพื่อส่งประกาศและการสื่อสารที่สำคัญ
• เรายังอาจใช้ข้อมูลส่วนบุคคลเพื่อวัตถุประสงค์ภายใน เช่น การดำเนินการตรวจสอบ การวิเคราะห์ข้อมูล และการวิจัยต่างๆ เพื่อปรับปรุงบริการที่เรามีให้และให้คำแนะนำเกี่ยวกับบริการของเราแก่คุณ
• หากคุณเข้าร่วมการจับรางวัล การประกวด หรือการส่งเสริมการขายที่คล้ายกัน เราอาจใช้ข้อมูลที่คุณให้ไว้เพื่อจัดการโปรแกรมดังกล่าว

การเปิดเผยข้อมูลแก่บุคคลที่สาม

เราไม่เปิดเผยข้อมูลที่ได้รับจากคุณต่อบุคคลที่สาม

ข้อยกเว้น:

• หากจำเป็น - ตามกฎหมาย ขั้นตอนการพิจารณาคดี ในการดำเนินการทางกฎหมาย และ/หรือตามคำขอสาธารณะหรือคำขอจากหน่วยงานของรัฐในอาณาเขตของสหพันธรัฐรัสเซีย - ให้เปิดเผยข้อมูลส่วนบุคคลของคุณ เรายังอาจเปิดเผยข้อมูลเกี่ยวกับคุณหากเราพิจารณาว่าการเปิดเผยดังกล่าวมีความจำเป็นหรือเหมาะสมเพื่อความปลอดภัย การบังคับใช้กฎหมาย หรือวัตถุประสงค์ที่สำคัญสาธารณะอื่น ๆ
• ในกรณีของการปรับโครงสร้างองค์กร การควบรวมกิจการ หรือการขาย เราอาจถ่ายโอนข้อมูลส่วนบุคคลที่เรารวบรวมไปยังบุคคลที่สามที่รับช่วงต่อที่เกี่ยวข้อง

การคุ้มครองข้อมูลส่วนบุคคล

เราใช้ความระมัดระวัง - รวมถึงการบริหารจัดการ ทางเทคนิค และทางกายภาพ - เพื่อปกป้องข้อมูลส่วนบุคคลของคุณจากการสูญหาย การโจรกรรม และการใช้งานในทางที่ผิด รวมถึงการเข้าถึง การเปิดเผย การเปลี่ยนแปลง และการทำลายโดยไม่ได้รับอนุญาต

การเคารพความเป็นส่วนตัวของคุณในระดับบริษัท

เพื่อให้มั่นใจว่าข้อมูลส่วนบุคคลของคุณปลอดภัย เราจะสื่อสารมาตรฐานความเป็นส่วนตัวและความปลอดภัยให้กับพนักงานของเรา และบังคับใช้หลักปฏิบัติด้านความเป็นส่วนตัวอย่างเคร่งครัด

บันทึก r b r = บันทึก ขหรือ เข้าสู่ระบบข= เข้าสู่ระบบ r b r

ค่าของลอการิทึมจะไม่เปลี่ยนแปลงหากฐานของลอการิทึมและตัวเลขใต้เครื่องหมายลอการิทึมถูกยกกำลังเท่ากัน

เฉพาะจำนวนบวกเท่านั้นที่สามารถอยู่ใต้เครื่องหมายลอการิทึม และฐานของลอการิทึมไม่เท่ากับหนึ่ง

ตัวอย่าง.

1) เปรียบเทียบบันทึก 3 9 และบันทึก 9 81

บันทึก 3 9=2 เนื่องจาก 3 2 =9;

บันทึก 9 81=2 เนื่องจาก 9 2 =81

ดังนั้น ล็อก 3 9=ล็อก 9 81

โปรดทราบว่าฐานของลอการิทึมที่สองมีค่าเท่ากับกำลังสองของฐานของลอการิทึมแรก: 9=3 2 และตัวเลขภายใต้เครื่องหมายของลอการิทึมที่สองจะเท่ากับกำลังสองของตัวเลขภายใต้เครื่องหมายของตัวแรก ลอการิทึม: 81=9 2. ปรากฎว่าทั้งตัวเลขและฐานของบันทึกลอการิทึมแรก 3 9 ถูกยกกำลังสอง และค่าของลอการิทึมไม่เปลี่ยนแปลงไปจากนี้:

ต่อไปตั้งแต่ทำการแตกราก nระดับจากหมู่ กคือการเพิ่มจำนวน กในระดับ ( 1/น) จากนั้นจากบันทึก 9 81 คุณจะได้รับบันทึก 3 9 โดยหารากที่สองของตัวเลขและฐานของลอการิทึม:

2) ตรวจสอบความเท่าเทียมกัน: บันทึก 4 25=บันทึก 0.5 0.2

ลองดูที่ลอการิทึมแรก หารากที่สองของฐาน 4 และจากหมู่นั้น 25 ; เราได้รับ: บันทึก 4 25=บันทึก 2 5

ลองดูที่ลอการิทึมที่สอง ฐานลอการิทึม: 0.5= 1/2 ตัวเลขใต้เครื่องหมายลอการิทึมนี้: 0.2= 1/5 ลองเพิ่มตัวเลขแต่ละตัวเหล่านี้ให้เป็นลบยกกำลังแรก:

0,5 -1 =(1 / 2) -1 =2;

0,2 -1 =(1 / 5) -1 =5.

ดังนั้น ล็อก 0.5 0.2=ล็อก 2 5 สรุป: ความเท่าเทียมกันนี้เป็นจริง

แก้สมการ:

บันทึก 4 x 4 +บันทึก 16 81=บันทึก 2 (5x+2)ลองลดลอการิทึมจากซ้ายไปที่ฐานกัน 2 .

บันทึก 2 x 2 +บันทึก 2 3=บันทึก 2 (5x+2) หารากที่สองของตัวเลขและฐานของลอการิทึมแรก แยกรากที่สี่ของตัวเลขและฐานของลอการิทึมที่สอง

บันทึก 2 (3x 2)=บันทึก 2 (5x+2) แปลงผลรวมของลอการิทึมเป็นลอการิทึมของผลิตภัณฑ์

3x 2 = 5x+2 ได้รับหลังจากการเสริมพลัง

3x 2 -5x-2=0. เราแก้สมการกำลังสองโดยใช้สูตรทั่วไปสำหรับสมการกำลังสองที่สมบูรณ์:

ก=3, ข=-5, ค=-2

D=b 2 -4ac=(-5) 2 -4∙3∙(-2)=25+24=49=7 2 >0; 2 รากที่แท้จริง

การตรวจสอบ.

x=2.

บันทึก 4 2 4 +บันทึก 16 81=บันทึก 2 (5∙2+2);

บันทึก 2 2 2 +บันทึก 2 3=บันทึก 2 12;

บันทึก 2 (4∙3)=บันทึก 2 12;

บันทึก 2 12=บันทึก 2 12;

เข้าสู่ระบบ n b=(1/ n)∙ เข้าสู่ระบบข

ลอการิทึมของตัวเลข ขขึ้นอยู่กับ หนึ่งเท่ากับผลคูณของเศษส่วน 1/ nถึงลอการิทึมของตัวเลข ขขึ้นอยู่กับ ก.

หา:1) 21ล็อก 8 3+40ล็อก 25 2; 2) 30log 32 3∙log 125 2 ถ้ามันรู้อย่างนั้น ล็อก 2 3=ข,บันทึก 5 2=ค.

สารละลาย.

แก้สมการ:

1) บันทึก 2 x+บันทึก 4 x+บันทึก 16 x=5.25

สารละลาย.

ลองลดลอการิทึมเหล่านี้เป็นฐาน 2 ใช้สูตร: เข้าสู่ระบบ n b=(1/ n)∙ เข้าสู่ระบบข

บันทึก 2 x+(½) บันทึก 2 x+(¼) บันทึก 2 x=5.25;

บันทึก 2 x+0.5 บันทึก 2 x+0.25 บันทึก 2 x=5.25 ต่อไปนี้เป็นคำที่คล้ายกัน:

(1+0.5+0.25) บันทึก 2 x=5.25;

1.75 บันทึก 2 x=5.25 |:1.75

บันทึก 2 x=3 ตามคำจำกัดความของลอการิทึม:

2) 0.5ล็อก 4 (x-2)+ล็อก 16 (x-3)=0.25

สารละลาย. ลองแปลงลอการิทึมเป็นฐาน 16 เป็นฐาน 4 กัน

0.5ล็อก 4 (x-2)+0.5ล็อก 4 (x-3)=0.25 |:0.5

บันทึก 4 (x-2)+บันทึก 4 (x-3)=0.5 ลองแปลงผลรวมของลอการิทึมเป็นลอการิทึมของผลิตภัณฑ์

บันทึก 4 ((x-2)(x-3))=0.5;

บันทึก 4 (x 2 -2x-3x+6)=0.5;

บันทึก 4 (x 2 -5x+6)=0.5 ตามคำจำกัดความของลอการิทึม:

x 2 -5x+4=0. ตามทฤษฎีบทของ Vieta:

x 1 =1; x 2 = 4. ค่าแรกของ x จะไม่ทำงาน เนื่องจากที่ x = 1 ลอการิทึมของความเท่าเทียมกันนี้ไม่มีอยู่ เนื่องจาก เฉพาะตัวเลขบวกเท่านั้นที่สามารถอยู่ใต้เครื่องหมายลอการิทึมได้

ลองตรวจสอบสมการนี้ที่ x=4

การตรวจสอบ.

0.5ล็อก 4 (4-2)+ล็อก 16 (4-3)=0.25

0.5ล็อก 4 2+ล็อก 16 1=0.25

0,5∙0,5+0=0,25

บันทึก a b=บันทึก c b/บันทึก c a

ลอการิทึมของตัวเลข ขขึ้นอยู่กับ กเท่ากับลอการิทึมของตัวเลข ขบนพื้นฐานใหม่ กับหารด้วยลอการิทึมของฐานเก่า กบนพื้นฐานใหม่ กับ.

ตัวอย่าง:

1) บันทึก 2 3=lg3/lg2;

2) บันทึก 8 7=ln7/ln8

คำนวณ:

1) บันทึก 5 7ถ้ามันรู้อย่างนั้น แอลจี7≈0,8451; แอลจี5≈0,6990.

คข / บันทึก คก.

บันทึก 5 7=log7/log5µ0.8451:0.6990µ1.2090

คำตอบ: บันทึก 5 7≈1,209 0≈1,209 .

2) บันทึก 5 7 ถ้ามันรู้อย่างนั้น ln7≈1,9459; ln5≈1,6094.

สารละลาย. ใช้สูตร: log a b =log คข / บันทึก คก.

บันทึก 5 7=ln7/ln5µ1.9459:1.6094µ1.2091

คำตอบ: บันทึก 5 7≈1,209 1≈1,209 .

ค้นหา x:

1) บันทึก 3 x=บันทึก 3 4+บันทึก 5 6/บันทึก 5 3+บันทึก 7 8/บันทึก 7 3

เราใช้สูตร: บันทึก คข / บันทึก คก = เข้าสู่ระบบข . เราได้รับ:

บันทึก 3 x=บันทึก 3 4+บันทึก 3 6+บันทึก 3 8;

บันทึก 3 x=บันทึก 3 (4∙6∙8);

บันทึก 3 x=บันทึก 3 192;

x=192 .

2) บันทึก 7 x=lg143-log 6 11/บันทึก 6 10-log 5 13/บันทึก 5 10.

เราใช้สูตร: บันทึก คข / บันทึก คก = เข้าสู่ระบบข เราได้รับ:

บันทึก 7 x=lg143-lg11-lg13;

บันทึก 7 x=lg143- (lg11+lg13);

บันทึก 7 x=lg143-lg (11∙13);

บันทึก 7 x=lg143-lg143;

x=1.

หน้า 1 จาก 1 1