ในบทเรียนที่แล้ว เราใช้สามขั้นตอนในการแก้สมการ

ขั้นตอนแรกคือด้านเทคนิค ด้วยการใช้ห่วงโซ่ของการแปลงจากสมการดั้งเดิม เราก็มาถึงสมการที่ค่อนข้างง่าย ซึ่งเราจะแก้และหาราก

ขั้นตอนที่สองคือการวิเคราะห์โซลูชัน เราวิเคราะห์การเปลี่ยนแปลงที่เราทำและค้นหาว่าการเปลี่ยนแปลงนั้นเทียบเท่ากันหรือไม่

ขั้นตอนที่สามคือการตรวจสอบ การตรวจสอบรากที่พบทั้งหมดโดยการแทนที่ลงในสมการดั้งเดิมเป็นสิ่งจำเป็นเมื่อทำการแปลงที่อาจนำไปสู่สมการที่พิสูจน์ได้

จำเป็นต้องแยกแยะสามขั้นตอนเสมอเมื่อแก้สมการหรือไม่?

ไม่แน่นอน เช่นในการแก้สมการนี้ ในชีวิตประจำวันมักไม่แยกแยะ แต่ขั้นตอนทั้งหมดเหล่านี้จำเป็นต้อง "คำนึงถึง" และดำเนินการในรูปแบบใดรูปแบบหนึ่ง จำเป็นต้องวิเคราะห์ความเท่าเทียมกันของการแปลง และหากการวิเคราะห์แสดงให้เห็นว่าจำเป็นต้องดำเนินการตรวจสอบ ก็ถือเป็นข้อบังคับ มิฉะนั้นจะไม่สามารถพิจารณาแก้สมการได้อย่างถูกต้อง

เป็นไปได้ไหมที่จะตรวจสอบรากของสมการด้วยการแทนที่เท่านั้น?

หากใช้การแปลงที่เท่ากันในการแก้สมการ ก็ไม่จำเป็นต้องตรวจสอบ เมื่อตรวจสอบรากของสมการ มักจะใช้ ODZ (ช่วงค่าที่อนุญาต) บ่อยครั้ง หากตรวจสอบโดยใช้ ODZ ได้ยาก ก็จะดำเนินการโดยการแทนที่ลงในสมการดั้งเดิม

แบบฝึกหัดที่ 1

แก้สมการรากที่สองของสอง x บวกสามเท่ากับหนึ่งบวก x

สารละลาย

ODZ ของสมการถูกกำหนดโดยระบบของอสมการสองตัว: สอง x บวกสามมากกว่าหรือเท่ากับศูนย์ และหนึ่งบวก x มากกว่าหรือเท่ากับศูนย์ ผลเฉลยคือ x มากกว่าหรือเท่ากับลบ 1

ลองยกกำลังสองข้างของสมการ ย้ายเทอมจากด้านหนึ่งของสมการไปอีกด้านหนึ่ง เพิ่มเทอมที่คล้ายกัน แล้วได้สมการกำลังสอง x กำลังสองเท่ากับสอง รากของมันคือ

x อันแรก อันที่สอง เท่ากับบวกหรือลบสแควร์รูทของสอง

การตรวจสอบ

ค่าของ x ตัวแรกเท่ากับรากที่สองของสองคือรากของสมการ เนื่องจากค่าดังกล่าวรวมอยู่ใน ODZ
ค่าของ x วินาทีเท่ากับลบรากที่สองของสอง ไม่ใช่รากของสมการ เพราะ มันไม่รวมอยู่ใน DZ
ลองตรวจสอบว่ารูท x เท่ากับสแควร์รูทของ 2 แล้วแทนที่มันลงในความเท่าเทียมกันดั้งเดิม เราจะได้

ความเท่าเทียมกันเป็นจริง ซึ่งหมายความว่า x เท่ากับรากที่สองของสองคือรากของสมการ

คำตอบ: รากที่สองของสอง

ภารกิจที่ 2

แก้สมการรากที่สองของ x ลบ 8 เท่ากับ 5 ลบ x

สารละลาย

ODZ ของสมการไม่ลงตัวถูกกำหนดโดยระบบของอสมการสองตัว: x ลบแปดมากกว่าหรือเท่ากับศูนย์ และห้าลบ x มากกว่าหรือเท่ากับศูนย์ เมื่อแก้ไขแล้วเราพบว่าระบบนี้ไม่มีวิธีแก้ปัญหา รากของสมการไม่สามารถเป็นค่าใดๆ ของตัวแปร x ได้

คำตอบ: ไม่มีราก

ภารกิจที่ 3

แก้สมการรากที่สองของ x กำลังสาม บวก 4 x ลบ 1 ลบ 8 รากที่สองของ x กำลังสี่ ลบ x เท่ากับรากที่สองของ x กำลังสาม ลบ 1 บวก 2 รากที่สองของ x

สารละลาย

การค้นหา ODZ ในสมการนี้ค่อนข้างยาก

เรามาทำการแปลงกัน: ยกกำลังสองทั้งสองข้างของสมการนี้

ลองย้ายพจน์ทั้งหมดไปทางซ้ายของสมการแล้วนำพจน์ที่เหมือนกัน เขียนรากสองตัวไว้ใต้รากเดียว ได้รากที่คล้ายกัน นำรากที่เหมือนกัน หารด้วยสัมประสิทธิ์ลบ 12 และแยกตัวประกอบนิพจน์ราก เราจะได้สมการใน รูปผลคูณของตัวประกอบสองตัวเท่ากับศูนย์ เมื่อแก้ไขแล้วเราจะพบราก:

x อันแรกเท่ากับหนึ่ง x วินาทีเท่ากับศูนย์

เนื่องจากเรายกสมการทั้งสองข้างขึ้นเป็นกำลังเท่ากัน การตรวจสอบรากจึงเป็นสิ่งจำเป็น

การตรวจสอบ

ถ้า x เท่ากับ 1 แล้ว

เราได้ความเท่าเทียมกันที่ถูกต้อง ซึ่งหมายความว่า x เท่ากับ 1 คือรากของสมการ

ถ้า x เป็นศูนย์ แล้วรากที่สองของลบหนึ่งจะนิยามไม่ได้

ซึ่งหมายความว่า x เท่ากับศูนย์คือรากที่ไม่เกี่ยวข้อง

คำตอบ: หนึ่ง

ภารกิจที่ 4

แก้สมการลอการิทึมของนิพจน์ x กำลังสองบวกห้า x บวกสองฐานสองเท่ากับสาม

สารละลาย

ลองหาสมการ ODZ กัน ในการทำสิ่งนี้ เราแก้อสมการ x กำลังสอง บวก 5 x บวก 2 ส่วน 0

เราแก้อสมการโดยใช้วิธีช่วงเวลา ในการทำเช่นนี้ เราแยกตัวประกอบทางด้านซ้ายของมัน โดยแก้สมการกำลังสองไปก่อนหน้านี้แล้ว และเมื่อคำนึงถึงเครื่องหมายอสมการแล้ว เราจะกำหนด ODZ ODZ เท่ากับการรวมกันของรังสีเปิดจากลบอนันต์ถึงลบเศษส่วนห้าบวกรากที่สองของสิบเจ็ดหารด้วยสอง และจากลบเศษส่วนห้าลบรากที่สองของสิบเจ็ดหารด้วยสองถึงบวกอนันต์

ตอนนี้เรามาเริ่มค้นหารากของสมการกันดีกว่า เมื่อพิจารณาว่า 3 เท่ากับลอการิทึมของ 8 ถึงฐาน 2 เราจึงเขียนสมการได้ดังนี้ ลอการิทึมของนิพจน์ x กำลังสองบวก 5 x บวก 2 ถึงฐาน 2 เท่ากับลอการิทึมของ 8 ถึงฐาน 2 ขอให้เราเสริมกำลังสมการ รับและแก้สมการกำลังสอง

ผู้เลือกปฏิบัติคือสี่สิบเก้า

คำนวณราก:

x อันแรกเท่ากับลบหก; x วินาทีเท่ากับหนึ่ง

การตรวจสอบ

ลบหกเป็นของ ODZ หนึ่งตัวเป็นของ ODZ ซึ่งหมายความว่าตัวเลขทั้งสองเป็นรากของสมการ

คำตอบ: ลบหก; หนึ่ง.

ในบทเรียนที่แล้ว เราได้พิจารณาถึงปัญหาการปรากฏตัวของรากภายนอก เราสามารถตรวจจับได้ผ่านการตรวจสอบ เป็นไปได้ไหมที่จะสูญเสียรากเมื่อแก้สมการและจะป้องกันได้อย่างไร?

เมื่อดำเนินการดังกล่าวกับสมการ เช่น ประการแรก หารทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน ax จาก x (ยกเว้นกรณีที่ทราบแน่ชัดว่า ax จาก x ไม่เท่ากับศูนย์สำหรับ x ใดๆ จาก ขอบเขตของนิยามของสมการ) ;

ประการที่สอง การลด OD ของสมการให้แคบลงในระหว่างกระบวนการแก้ปัญหาอาจทำให้สูญเสียรากของสมการได้

จดจำ!

สมการที่เขียนเป็น

ef จาก x คูณด้วยเถ้าจาก x เท่ากับ zhe จาก x คูณด้วยเถ้าจาก x ได้รับการแก้ไขด้วยวิธีนี้:

คุณต้องแยกตัวประกอบโดยนำตัวประกอบร่วมออกจากวงเล็บ

จากนั้นให้แบ่งแต่ละปัจจัยให้เป็นศูนย์ จะได้สมการสองสมการ

เราคำนวณรากของพวกเขา

แบบฝึกหัดที่ 1

แก้สมการ x ลูกบาศก์เท่ากับ x

วิธีแรก

หารทั้งสองข้างของสมการด้วย x เราจะได้ x กำลังสองเท่ากับ 1 มีราก x ก่อนเท่ากับ 1

x วินาทีเท่ากับลบหนึ่ง

วิธีที่สอง

X คิวบ์เท่ากับ X ลองย้าย x ไปทางซ้ายของสมการ นำ x ออกจากวงเล็บ แล้วเราจะได้: x คูณด้วย x กำลังสอง ลบ 1 เท่ากับ 0

ลองคำนวณรากของมัน:

X อันแรกเท่ากับศูนย์ x วินาทีเท่ากับหนึ่ง x อันที่สามเท่ากับลบหนึ่ง

สมการนี้มีสามราก

เมื่อแก้ไขวิธีแรก เราสูญเสียหนึ่งรูต - x เท่ากับศูนย์

คำตอบ: ลบหนึ่ง; ศูนย์; หนึ่ง.

จดจำ! การลดทั้งสองด้านของสมการด้วยปัจจัยที่ไม่ทราบค่าอาจทำให้สูญเสียรากได้

ภารกิจที่ 2

แก้สมการ: ลอการิทึมฐานสิบของ x กำลังสองเท่ากับสอง

สารละลาย

วิธีแรก

ตามคำจำกัดความของลอการิทึม เราจะได้สมการกำลังสอง x กำลังสองเท่ากับหนึ่งร้อย

รากของมัน: x แรกเท่ากับสิบ; X วินาทีเท่ากับลบสิบ

วิธีที่สอง

โดยสมบัติของลอการิทึม เรามีลอการิทึมฐานสิบสอง x เท่ากับสอง

รากของมัน - x เท่ากับสิบ

ด้วยวิธีที่สอง ราก x เท่ากับลบสิบหายไป และเหตุผลก็คือพวกเขาใช้สูตรผิด ทำให้ขอบเขตของสมการแคบลง นิพจน์สำหรับลอการิทึมฐานสิบของ x กำลังสองถูกกำหนดไว้สำหรับ x ทั้งหมดยกเว้น x เท่ากับศูนย์ นิพจน์สำหรับลอการิทึมฐานสิบของ x คือค่า x ที่มากกว่าศูนย์ สูตรที่ถูกต้องสำหรับลอการิทึมฐานสิบ x กำลังสองเท่ากับโมดูลลอการิทึมฐานสิบสอง x

จดจำ! เมื่อแก้สมการ ให้ใช้สูตรที่มีอยู่อย่างชาญฉลาด

การแปลงต่อไปนี้มักใช้เมื่อแก้สมการ:

การเปลี่ยนแปลงอื่น ๆ

ในรายการที่นำเสนอในย่อหน้าก่อนหน้านี้ เราจงใจไม่รวมการแปลง เช่น การยกสมการทั้งสองข้างให้มีกำลังธรรมชาติเท่ากัน ลอการิทึม การเสริมกำลังทั้งสองด้านของสมการ การดึงรากที่มีระดับเดียวกันออกจากทั้งสองด้านของสมการ สมการ การปล่อยฟังก์ชันภายนอก และอื่นๆ ความจริงก็คือการแปลงเหล่านี้ไม่ได้เป็นเรื่องทั่วไป: การแปลงจากรายการด้านบนใช้ในการแก้สมการทุกประเภท และการแปลงที่กล่าวถึงข้างต้นใช้ในการแก้สมการบางประเภท (ไม่ลงตัว, เอ็กซ์โปเนนเชียล, ลอการิทึม ฯลฯ ) พวกเขาจะกล่าวถึงรายละเอียดภายในกรอบของวิธีการที่เกี่ยวข้องในการแก้สมการประเภทที่เกี่ยวข้อง นี่คือลิงก์ไปยังคำอธิบายโดยละเอียด:

• การยกสมการทั้งสองข้างให้มีกำลังธรรมชาติเท่ากัน
• หาลอการิทึมของทั้งสองข้างของสมการ.
• ศักยภาพทั้งสองด้านของสมการ.
• การแยกรากของกำลังเท่ากันจากทั้งสองข้างของสมการ.
• การแทนที่นิพจน์ที่สอดคล้องกับส่วนหนึ่งของสมการดั้งเดิมด้วยนิพจน์จากอีกส่วนหนึ่งของสมการดั้งเดิม.

ลิงก์ที่ให้มาประกอบด้วยข้อมูลที่ครอบคลุมเกี่ยวกับการเปลี่ยนแปลงที่ระบุไว้ ดังนั้นเราจะไม่พูดถึงพวกเขาในบทความนี้อีกต่อไป ข้อมูลที่ตามมาทั้งหมดใช้กับการแปลงจากรายการการแปลงพื้นฐาน

จะเกิดอะไรขึ้นจากการแปลงสมการ?

การทำการแปลงข้างต้นทั้งหมดสามารถให้สมการที่มีรากเดียวกันกับสมการดั้งเดิม หรือสมการที่รากมีรากทั้งหมดของสมการดั้งเดิม แต่อาจมีรากอื่นด้วย หรือสมการที่รากไม่มี รวมรากทั้งหมดของสมการที่แปลงแล้ว ในย่อหน้าต่อไปนี้ เราจะวิเคราะห์ว่าการแปลงใดต่อไปนี้ จะนำไปสู่สมการใดภายใต้เงื่อนไขใด นี่เป็นสิ่งสำคัญอย่างยิ่งที่ต้องรู้เพื่อการแก้สมการได้สำเร็จ

การแปลงสมการที่เท่ากัน

สิ่งที่น่าสนใจเป็นพิเศษคือการแปลงสมการที่ทำให้เกิดสมการที่เท่ากัน กล่าวคือ สมการที่มีรากชุดเดียวกันกับสมการดั้งเดิม การเปลี่ยนแปลงดังกล่าวเรียกว่า การแปลงที่เท่ากัน. ในหนังสือเรียนของโรงเรียนไม่ได้ให้คำจำกัดความที่เกี่ยวข้องไว้อย่างชัดเจน แต่สามารถอ่านได้ง่ายจากบริบท:

คำนิยาม

การแปลงสมการที่เท่ากันคือการแปลงที่ให้สมการที่เท่ากัน

แล้วเหตุใดการแปลงที่เท่ากันจึงน่าสนใจ? ความจริงก็คือถ้าด้วยความช่วยเหลือของพวกเขา มันเป็นไปได้ที่จะมาจากสมการที่กำลังแก้เป็นสมการเทียบเท่าที่ค่อนข้างง่าย การแก้สมการนี้จะให้คำตอบที่ต้องการกับสมการดั้งเดิม

จากการเปลี่ยนแปลงที่ระบุไว้ในย่อหน้าก่อนหน้านี้ ไม่ใช่ทั้งหมดจะเท่ากันเสมอไป การแปลงบางอย่างจะเทียบเท่ากันภายใต้เงื่อนไขบางประการเท่านั้น เรามาสร้างรายการข้อความที่กำหนดว่าการแปลงใดและภายใต้เงื่อนไขใดที่เป็นการแปลงสมการที่เทียบเท่ากัน ในการทำเช่นนี้ เราจะใช้รายการข้างต้นเป็นพื้นฐาน และสำหรับการแปลงที่ไม่เท่ากันเสมอไป เราจะเพิ่มเงื่อนไขที่ให้ความเท่าเทียมกัน นี่คือรายการ:

• การแทนที่นิพจน์ทางด้านซ้ายหรือด้านขวาของสมการด้วยนิพจน์ที่ไม่เปลี่ยนตัวแปรของสมการถือเป็นการแปลงสมการที่เทียบเท่ากัน

ให้เราอธิบายว่าทำไมจึงเป็นเช่นนี้ ในการทำเช่นนี้ เราใช้สมการที่มีตัวแปรตัวเดียว (การใช้เหตุผลที่คล้ายกันสามารถทำได้สำหรับสมการที่มีตัวแปรหลายตัว) ในรูปแบบ A(x)=B(x) เราแสดงนิพจน์ทางด้านซ้ายและด้านขวาเป็น A( x) และ B(x) ตามลำดับ ปล่อยให้นิพจน์ C(x) เท่ากันกับนิพจน์ A(x) และ ODZ ของตัวแปร x ของสมการ C(x)=B(x) เกิดขึ้นพร้อมกับ ODZ ของตัวแปร x สำหรับสมการดั้งเดิม ให้เราพิสูจน์ว่าการแปลงสมการ A(x)=B(x) ไปเป็นสมการ C(x)=B(x) เป็นการแปลงที่เท่ากัน นั่นคือ เราจะพิสูจน์ว่าสมการ A(x)=B (x) และ C(x) =B(x) เทียบเท่ากัน

ในการทำเช่นนี้ ก็เพียงพอที่จะแสดงว่ารากใดๆ ของสมการดั้งเดิมคือรากของสมการ C(x)=B(x) และรากใดๆ ของสมการ C(x)=B(x) นั้นเป็นราก ของสมการเดิม

เริ่มจากส่วนแรกกันก่อน ให้ q เป็นรากของสมการ A(x)=B(x) จากนั้นเมื่อเราแทนที่มันด้วย x เราจะได้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง A(q)=B(q) เนื่องจากนิพจน์ A(x) และ C(x) เท่ากัน และนิพจน์ C(q) ก็สมเหตุสมผล (ซึ่งตามมาจากเงื่อนไขที่ว่า OD สำหรับสมการ C(x)=B(x) เกิดขึ้นพร้อมกับ OD สำหรับ สมการดั้งเดิม) จากนั้นความเท่าเทียมกันเชิงตัวเลข A(q)=C(q) เป็นจริง ต่อไปเราจะใช้คุณสมบัติของความเท่าเทียมกันของตัวเลข เนื่องจากคุณสมบัติสมมาตร ความเท่าเทียมกัน A(q)=C(q) จึงสามารถเขียนใหม่เป็น C(q)=A(q) ได้ จากนั้น เนื่องจากคุณสมบัติการส่งผ่าน ความเท่าเทียมกัน C(q)=A(q) และ A(q)=B(q) บ่งบอกถึงความเท่าเทียมกัน C(q)=B(q) นี่พิสูจน์ว่า q คือรากของสมการ C(x)=B(x)

ส่วนที่สองและข้อความทั้งหมดโดยรวม ได้รับการพิสูจน์ในลักษณะที่คล้ายคลึงกันโดยสิ้นเชิง

สาระสำคัญของการแปลงที่เทียบเท่าที่วิเคราะห์มีดังนี้: ช่วยให้คุณสามารถทำงานแยกกันด้วยนิพจน์ทางด้านซ้ายและด้านขวาของสมการ โดยแทนที่ด้วยนิพจน์ที่เท่ากันใน ODZ ดั้งเดิมของตัวแปร

ตัวอย่างที่พบบ่อยที่สุด: เราสามารถแทนที่ผลรวมของตัวเลขทางด้านขวาของสมการ x=2+1 ด้วยค่าของมัน ซึ่งจะส่งผลให้ได้สมการที่เทียบเท่ากันในรูปแบบ x=3 อันที่จริง เราได้แทนที่นิพจน์ 2+1 ด้วยนิพจน์ 3 ที่เท่ากันและ ODZ ของสมการไม่เปลี่ยนแปลง อีกตัวอย่างหนึ่ง: ทางด้านซ้ายของสมการ 3·(x+2)=7·x−2·x+4−1 เราทำได้ และทางขวา – ซึ่งจะนำเราไปสู่สมการที่เทียบเท่า 3·x+ 6=5·x+ 3. สมการที่ได้นั้นเทียบเท่ากันอย่างแน่นอน เนื่องจากเราแทนที่นิพจน์ด้วยนิพจน์ที่เท่ากันและในเวลาเดียวกันก็ได้สมการที่มี OD ที่ตรงกับ OD สำหรับสมการดั้งเดิม

• การบวกจำนวนเดียวกันทั้งสองข้างของสมการหรือการลบจำนวนเดียวกันออกจากทั้งสองข้างของสมการถือเป็นการแปลงสมการที่เท่ากัน

ขอให้เราพิสูจน์ว่าการบวกเลข c ที่เท่ากันทั้งสองข้างของสมการ A(x)=B(x) จะได้สมการที่เทียบเท่า A(x)+c=B(x)+c และค่าที่ลบออกจากทั้งสองด้านของสมการ A(x) =B(x) ของจำนวนเดียวกัน c ให้สมการที่เทียบเท่า A(x)−c=B(x)−c

ให้ q เป็นรากของสมการ A(x)=B(x) แล้วความเท่าเทียมกัน A(q)=B(q) เป็นจริง คุณสมบัติของความเท่าเทียมกันของตัวเลขทำให้เราสามารถเพิ่มทั้งสองด้านของความเท่าเทียมกันของตัวเลขจริงหรือลบตัวเลขเดียวกันออกจากส่วนต่างๆ ให้เราแสดงว่าจำนวนนี้เป็น c แล้วความเท่าเทียมกัน A(q)+c=B(q)+c และ A(q)−c=B(q)−c ใช้ได้ จากความเท่าเทียมกันเหล่านี้ q คือรากของสมการ A(x)+c=B(x)+c และสมการ A(x)−c=B(x)−c

ตอนนี้กลับมาแล้ว ให้ q เป็นรากของสมการ A(x)+c=B(x)+c และสมการ A(x)−c=B(x)−c จากนั้น A(q)+c=B(q) +c และ A (q)−c=B(q)−c เรารู้ว่าการลบจำนวนเดียวกันออกจากทั้งสองด้านของความเท่าเทียมกันของตัวเลขที่แท้จริงจะทำให้เกิดความเท่าเทียมกันของตัวเลขที่แท้จริง เรายังรู้ด้วยว่าการบวกความเท่าเทียมกันของตัวเลขที่ถูกต้องทั้งสองข้างจะทำให้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง ขอให้เราลบเลข c ออกจากทั้งสองด้านของความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q)+c=B(q)+c และเพิ่มตัวเลข c เข้ากับทั้งสองด้านของความเท่าเทียมกัน A(x)−c=B(x) −ค นี่จะทำให้เรามีความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q)+c−c=B(q)+c−c และ A(q)−c+c=B(q)+c−c ซึ่งเราจะสรุปได้ว่า A (คิว) =B(q) . จากความเท่าเทียมกันครั้งล่าสุด q คือรากของสมการ A(x)=B(x)

นี่เป็นการพิสูจน์ข้อความดั้งเดิมโดยรวม

ให้เรายกตัวอย่างการเปลี่ยนแปลงสมการดังกล่าว ลองใช้สมการ x−3=1 แล้วแปลงมันโดยบวกเลข 3 ทั้งสองข้าง หลังจากนั้นเราจะได้สมการ x−3+3=1+3 ซึ่งเทียบเท่ากับสมการดั้งเดิม เห็นได้ชัดว่าในสมการผลลัพธ์ คุณสามารถดำเนินการกับตัวเลขได้ ดังที่เราได้คุยกันไปแล้วในรายการก่อนหน้า ดังนั้นเราจึงได้สมการ x=4 ดังนั้น ในการทำการแปลงที่เท่ากัน เราแก้สมการโดยไม่ได้ตั้งใจ x−3=1 รากของมันคือเลข 4 การแปลงที่เทียบเท่าที่พิจารณามักใช้เพื่อกำจัดพจน์ตัวเลขที่เหมือนกันซึ่งอยู่ในส่วนต่างๆ ของสมการ ตัวอย่างเช่น ทั้งด้านซ้ายและด้านขวาของสมการ x 2 +1=x+1 มีพจน์ 1 เหมือนกัน การลบเลข 1 จากทั้งสองข้างของสมการจะทำให้เราสามารถไปยังสมการที่เทียบเท่า x 2 + 1−1=x+1−1 และต่อจากสมการที่เทียบเท่า x 2 =x และด้วยเหตุนี้จึงกำจัดพจน์ที่เหมือนกันเหล่านี้ออกไป

• การเพิ่มทั้งสองด้านของสมการหรือการลบออกจากทั้งสองด้านของสมการ นิพจน์ที่ ODZ ไม่แคบกว่า ODZ สำหรับสมการดั้งเดิมจะเป็นการแปลงที่เทียบเท่ากัน

ลองพิสูจน์ข้อความนี้กัน นั่นคือ เราพิสูจน์ว่าสมการ A(x)=B(x) และ A(x)+C(x)=B(x)+C(x) เท่ากัน โดยมีเงื่อนไขว่า ODZ สำหรับนิพจน์ C(x) ) ไม่ใช่อยู่แล้ว เกินกว่า ODZ สำหรับสมการ A(x)=B(x)

ก่อนอื่นเราพิสูจน์จุดเสริมหนึ่งจุด ให้เราพิสูจน์ว่าภายใต้เงื่อนไขที่กำหนด สมการ OD ก่อนและหลังการแปลงจะเหมือนกัน แท้จริงแล้ว ODZ สำหรับสมการ A(x)+C(x)=B(x)+C(x) ถือได้ว่าเป็นจุดตัดของ ODZ สำหรับสมการ A(x)=B(x) และ ODZ สำหรับนิพจน์ C(x) . จากนี้และจากข้อเท็จจริงที่ว่า ODZ สำหรับนิพจน์ C(x) ไม่ได้แคบตามเงื่อนไขมากกว่า ODZ สำหรับสมการ A(x)=B(x) จึงตามมาด้วยว่า ODZ สำหรับสมการ A(x)= B(x) และ A (x)+C(x)=B(x)+C(x) เหมือนกัน

ตอนนี้เราจะพิสูจน์ความเท่าเทียมกันของสมการ A(x)=B(x) และ A(x)+C(x)=B(x)+C(x) โดยมีเงื่อนไขว่าช่วงของค่าที่ยอมรับได้สำหรับสิ่งเหล่านี้ สมการก็เหมือนกัน เราจะไม่พิสูจน์ความเท่าเทียมกันของสมการ A(x)=B(x) และ A(x)−C(x)=B(x)−C(x) ภายใต้เงื่อนไขที่ระบุ เนื่องจากเงื่อนไขจะคล้ายกัน .

ให้ q เป็นรากของสมการ A(x)=B(x) แล้วความเท่าเทียมกันเชิงตัวเลข A(q)=B(q) เป็นจริง เนื่องจาก ODZ ของสมการ A(x)=B(x) และ A(x)+C(x)=B(x)+C(x) เหมือนกัน ดังนั้นนิพจน์ C(x) จึงสมเหตุสมผลที่ x =q ซึ่งหมายถึง C(q) คือตัวเลขจำนวนหนึ่ง หากเราบวก C(q) เข้ากับทั้งสองด้านของความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q)=B(q) สิ่งนี้จะให้ความไม่เท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q)+C(q)=B(q)+C(q ) ซึ่งตามหลังว่า q คือรากของสมการ A(x)+C(x)=B(x)+C(x)

กลับ. ให้ q เป็นรากของสมการ A(x)+C(x)=B(x)+C(x) แล้ว A(q)+C(q)=B(q)+C(q) คือ a ความเท่าเทียมกันของตัวเลขที่แท้จริง เรารู้ว่าการลบจำนวนเดียวกันออกจากทั้งสองด้านของความเท่าเทียมกันของตัวเลขที่แท้จริงจะทำให้เกิดความเท่าเทียมกันของตัวเลขที่แท้จริง ลบ C(q) จากทั้งสองด้านของความเท่าเทียมกัน A(q)+C(q)=B(q)+C(q) สิ่งนี้จะให้ A(q)+C(q)−C(q)=B(q)+C(q)−C(q)และต่อไป A(q)=B(q) ดังนั้น q คือรากของสมการ A(x)=B(x)

ดังนั้นข้อความที่เป็นปัญหาจึงได้รับการพิสูจน์อย่างสมบูรณ์

ลองยกตัวอย่างการแปลงนี้กัน ลองใช้สมการ 2 x+1=5 x+2 เราสามารถบวกทั้งสองข้างได้ เช่น นิพจน์ −x−1 การเพิ่มนิพจน์นี้จะไม่เปลี่ยน ODZ ซึ่งหมายความว่าการเปลี่ยนแปลงดังกล่าวจะเทียบเท่ากัน ด้วยเหตุนี้เราจึงได้สมการที่เทียบเท่ากัน 2 x+1+(−x−1)=5 x+2+(−x−1). สมการนี้สามารถแปลงเพิ่มเติมได้: เปิดวงเล็บและลดเงื่อนไขที่คล้ายกันทางด้านซ้ายและด้านขวา (ดูรายการแรกในรายการ) หลังจากดำเนินการเหล่านี้ เราจะได้สมการที่เทียบเท่า x=4·x+1 การแปลงสมการที่กำลังพิจารณามักใช้เพื่อกำจัดพจน์ที่เหมือนกันซึ่งอยู่ทางด้านซ้ายและด้านขวาของสมการพร้อมกัน

• หากคุณย้ายคำศัพท์ในสมการจากส่วนหนึ่งไปยังอีกส่วนหนึ่ง โดยเปลี่ยนเครื่องหมายของเทอมนี้ไปในทางตรงกันข้าม คุณจะได้สมการที่เทียบเท่ากับสมการที่กำหนด

คำสั่งนี้เป็นผลมาจากคำสั่งก่อนหน้า

ให้เราแสดงให้เห็นว่าการแปลงสมการที่เทียบเท่านี้ดำเนินการอย่างไร ลองใช้สมการ 3·x−1=2·x+3 กัน ลองย้ายคำเช่น 2 x จากด้านขวาไปทางซ้ายเพื่อเปลี่ยนเครื่องหมาย ในกรณีนี้ เราได้สมการที่เทียบเท่ากัน 3·x−1−2·x=3 คุณยังสามารถย้ายลบหนึ่งจากด้านซ้ายของสมการไปทางขวา โดยเปลี่ยนเครื่องหมายเป็นบวก: 3 x−2 x=3+1 ในที่สุด การนำพจน์ที่คล้ายกันมาทำให้เราได้สมการที่เทียบเท่า x=4

• การคูณหรือหารทั้งสองข้างของสมการด้วยจำนวนที่ไม่เป็นศูนย์เท่ากันถือเป็นการแปลงที่เท่ากัน

เรามาพิสูจน์กัน

ให้ A(x)=B(x) เป็นสมการและ c เป็นตัวเลขที่แตกต่างจากศูนย์ ขอให้เราพิสูจน์ว่าการคูณหรือหารทั้งสองข้างของสมการ A(x)=B(x) ด้วยจำนวน c เป็นการแปลงสมการที่เทียบเท่ากัน ในการทำเช่นนี้ เราพิสูจน์ว่าสมการ A(x)=B(x) และ A(x) c=B(x) c เช่นเดียวกับสมการ A(x)=B(x) และ A(x) :c= B(x):c - เทียบเท่า ซึ่งสามารถทำได้ด้วยวิธีนี้: พิสูจน์ว่ารากใดๆ ของสมการ A(x)=B(x) คือรากของสมการ A(x) c=B(x) c และรากของสมการ A(x) :c=B(x) :c แล้วพิสูจน์ว่ารากใดๆ ของสมการ A(x) c=B(x) c เช่นเดียวกับรากใดๆ ของสมการ A(x):c=B(x):c , เป็นรากของสมการ A(x) =B(x) มาทำกัน.

ให้ q เป็นรากของสมการ A(x)=B(x) . จากนั้นความเท่าเทียมกันของตัวเลข A(q)=B(q) เป็นจริง จากการศึกษาคุณสมบัติของความเท่าเทียมกันเชิงตัวเลข เราได้เรียนรู้ว่าการคูณหรือหารทั้งสองข้างของความเท่าเทียมกันเชิงตัวเลขที่แท้จริงด้วยจำนวนเดียวกันที่ไม่ใช่ศูนย์จะนำไปสู่ความเท่าเทียมกันเชิงตัวเลขที่แท้จริง เมื่อคูณทั้งสองข้างของความเท่าเทียมกัน A(q)=B(q) ด้วย c เราจะได้ความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q) c=B(q) c ซึ่งตามมาด้วยว่า q คือรากของสมการ A( x) ค= ข(x)·ค . และการหารทั้งสองข้างของความเท่าเทียมกัน A(q)=B(q) ด้วย c เราจะได้ความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q):c=B(q):c ซึ่งตามหลังว่า q คือรากของ สมการ A(x):c =B(x):c .

ตอนนี้ไปในทิศทางอื่น ให้ q เป็นรากของสมการ A(x) c=B(x) c จากนั้น A(q)·c=B(q)·c คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง เมื่อหารทั้งสองส่วนด้วยจำนวนที่ไม่ใช่ศูนย์ c เราจะได้ความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(q)·c:c=B(q)·c:c และ A(q)=B(q) เพิ่มเติม ตามมาว่า q คือรากของสมการ A(x)=B(x) ถ้า q เป็นรากของสมการ A(x):c=B(x):c จากนั้น A(q):c=B(q):c คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง เมื่อคูณทั้งสองส่วนด้วยตัวเลขที่ไม่ใช่ศูนย์ c เราจะได้ความเท่าเทียมกันทางตัวเลขที่ถูกต้อง A(q):c·c=B(q):c·c และต่อไป A(q)=B(q) ตามมาว่า q คือรากของสมการ A(x)=B(x)

คำกล่าวนี้ได้รับการพิสูจน์แล้ว

ลองยกตัวอย่างการแปลงนี้กัน ด้วยความช่วยเหลือ คุณสามารถกำจัดเศษส่วนในสมการได้ เมื่อต้องการทำเช่นนี้ คุณสามารถคูณทั้งสองข้างของสมการด้วย 12 ผลลัพธ์ที่ได้คือสมการที่เทียบเท่าของแบบฟอร์ม ซึ่งสามารถแปลงเป็นสมการที่เทียบเท่า 7 x−3=10 ซึ่งไม่มีเศษส่วนอยู่ในสัญกรณ์

• การคูณหรือหารทั้งสองด้านของสมการด้วยนิพจน์เดียวกัน OD ซึ่งไม่แคบกว่า OD สำหรับสมการดั้งเดิมและไม่หายไปจาก OD สำหรับสมการดั้งเดิม ถือเป็นการแปลงที่เทียบเท่ากัน

ลองพิสูจน์ข้อความนี้กัน ในการทำเช่นนี้ เราพิสูจน์ว่าถ้า ODZ สำหรับนิพจน์ C(x) ไม่แคบกว่า ODZ สำหรับสมการ A(x)=B(x) และ C(x) จะไม่หายไปบน ODZ สำหรับสมการ A(x)=B( x) จากนั้นสมการ A(x)=B(x) และ A(x) C(x)=B(x) C(x) เช่นเดียวกับสมการ A(x) =B(x) และ A( x):C(x)=B(x):C(x) - เทียบเท่า

ให้ q เป็นรากของสมการ A(x)=B(x) . จากนั้น A(q)=B(q) คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง จากข้อเท็จจริงที่ว่า ODZ สำหรับนิพจน์ C(x) ไม่ใช่ ODZ เดียวกันสำหรับสมการ A(x)=B(x) จึงเป็นไปตามที่นิพจน์ C(x) สมเหตุสมผลเมื่อ x=q ซึ่งหมายความว่า C(q) คือตัวเลขจำนวนหนึ่ง นอกจากนี้ C(q) ไม่เป็นศูนย์ ซึ่งตามมาจากเงื่อนไขที่ว่านิพจน์ C(x) จะไม่หายไป หากเราคูณทั้งสองด้านของความเท่ากัน A(q)=B(q) ด้วยตัวเลขที่ไม่ใช่ศูนย์ C(q) ก็จะได้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง A(q)·C(q)=B(q)· C(q) ซึ่งเป็นไปตามนั้น q คือรากของสมการ A(x)·C(x)=B(x)·C(x) หากเราหารทั้งสองข้างของความเท่ากัน A(q)=B(q) ด้วยจำนวนที่ไม่ใช่ศูนย์ C(q) จะได้ค่าความเท่าเทียมกันของตัวเลขที่ถูกต้อง A(q):C(q)=B(q): C(q) ซึ่งตามหลังว่า q คือรากของสมการ A(x):C(x)=B(x):C(x)

กลับ. ให้ q เป็นรากของสมการ A(x)·C(x)=B(x)·C(x) จากนั้น A(q)·C(q)=B(q)·C(q) คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง โปรดทราบว่า ODZ สำหรับสมการ A(x) C(x)=B(x) C(x) เหมือนกับ ODZ สำหรับสมการ A(x)=B(x) (เราให้เหตุผลในสมการข้อใดข้อหนึ่ง ย่อหน้าก่อนหน้ารายการปัจจุบัน) เนื่องจาก C(x) ตามเงื่อนไขไม่หายไปบน ODZ สำหรับสมการ A(x)=B(x) ดังนั้น C(q) จึงเป็นตัวเลขที่ไม่ใช่ศูนย์ การหารทั้งสองข้างของความเท่าเทียมกัน A(q) C(q)=B(q) C(q) ด้วยตัวเลขที่ไม่ใช่ศูนย์ C(q) เราจะได้ความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(คิว)·C(q):C(q)=B(q)·C(q):C(q)และต่อไป A(q)=B(q) ตามมาว่า q คือรากของสมการ A(x)=B(x) ถ้า q เป็นรากของสมการ A(x):C(x)=B(x):C(x) ดังนั้น A(q):C(q)=B(q):C(q) คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง การคูณทั้งสองด้านของความเท่าเทียมกัน A(q):C(q)=B(q):C(q) ด้วยตัวเลขที่ไม่ใช่ศูนย์ C(q) เราจะได้ความเท่าเทียมกันเชิงตัวเลขที่ถูกต้อง A(คิว):C(q)·C(q)=B(q):C(q)·C(q)และต่อไป A(q)=B(q) ตามมาว่า q คือรากของสมการ A(x)=B(x)

คำกล่าวนี้ได้รับการพิสูจน์แล้ว

เพื่อความชัดเจน เราจะยกตัวอย่างการดำเนินการแปลงแบบแยกส่วน ลองหารทั้งสองข้างของสมการ x 3 ·(x 2 +1)=8·(x 2 +1) ด้วยนิพจน์ x 2 +1 การแปลงนี้เทียบเท่ากัน เนื่องจากนิพจน์ x 2 +1 ไม่ได้หายไปบน OD สำหรับสมการดั้งเดิม และ OD ของนิพจน์นี้ไม่แคบกว่า OD สำหรับสมการดั้งเดิม จากผลของการเปลี่ยนแปลงนี้ เราได้สมการที่เทียบเท่ากัน x 3 ·(x 2 +1):(x 2 +1)=8·(x 2 +1):(x 2 +1)ซึ่งสามารถแปลงเป็นสมการที่เทียบเท่าได้อีก x 3 =8

การเปลี่ยนแปลงที่นำไปสู่สมการที่พิสูจน์ได้

ในย่อหน้าก่อนหน้านี้ เราได้ตรวจสอบว่าการแปลงใดจากรายการการแปลงพื้นฐานและภายใต้เงื่อนไขใดที่เทียบเท่ากัน ตอนนี้เรามาดูกันว่าการแปลงใดเหล่านี้และภายใต้เงื่อนไขใดที่นำไปสู่สมการที่พิสูจน์ได้นั่นคือสมการที่มีรากทั้งหมดของสมการที่ถูกแปลง แต่นอกเหนือจากนั้นอาจมีรากอื่นด้วย - รากที่ไม่เกี่ยวข้องสำหรับสมการดั้งเดิม

การเปลี่ยนแปลงที่นำไปสู่สมการที่พิสูจน์ได้นั้นเป็นที่ต้องการไม่น้อยไปกว่าการแปลงที่เทียบเท่ากัน หากด้วยความช่วยเหลือของพวกเขาเป็นไปได้ที่จะได้สมการที่ค่อนข้างง่ายในแง่ของการแก้ปัญหาดังนั้นการแก้ปัญหาและการกำจัดรากที่ไม่เกี่ยวข้องในภายหลังจะให้คำตอบกับสมการดั้งเดิม

โปรดทราบว่าการแปลงที่เท่ากันทั้งหมดถือได้ว่าเป็นกรณีพิเศษของการแปลงที่นำไปสู่สมการที่พิสูจน์ได้ สิ่งนี้สามารถเข้าใจได้ เนื่องจากสมการที่เทียบเท่ากันเป็นกรณีพิเศษของสมการที่เป็นผลพิสูจน์ แต่จากมุมมองเชิงปฏิบัติ จะมีประโยชน์มากกว่าที่จะรู้ว่าการเปลี่ยนแปลงที่อยู่ระหว่างการพิจารณานั้นเทียบเท่ากันอย่างแน่นอน และไม่นำไปสู่สมการที่พิสูจน์ได้ ให้เราอธิบายว่าทำไมจึงเป็นเช่นนี้ หากเรารู้ว่าการแปลงเท่ากัน สมการที่ได้จะไม่มีรากที่อยู่นอกสมการดั้งเดิมอย่างแน่นอน และการเปลี่ยนแปลงที่นำไปสู่สมการที่เป็นผลอาจเป็นสาเหตุของการปรากฏตัวของรากภายนอกซึ่งทำให้เราต้องดำเนินการเพิ่มเติมในอนาคต - การแยกรากที่ไม่เกี่ยวข้องออก ดังนั้นในส่วนนี้ของบทความเราจะเน้นไปที่การแปลงซึ่งเป็นผลมาจากรากที่ไม่เกี่ยวข้องอาจปรากฏขึ้นสำหรับสมการดั้งเดิม และเป็นสิ่งสำคัญอย่างยิ่งที่จะต้องสามารถแยกแยะการเปลี่ยนแปลงดังกล่าวจากการแปลงที่เทียบเท่ากันเพื่อทำความเข้าใจอย่างชัดเจนว่าเมื่อใดจำเป็นต้องกรองรากที่ไม่เกี่ยวข้องออก และเมื่อใดที่ไม่จำเป็น

มาวิเคราะห์รายการการแปลงสมการพื้นฐานทั้งหมดที่ระบุในย่อหน้าที่สองของบทความนี้เพื่อค้นหาการแปลงอันเป็นผลมาจากรากที่ไม่เกี่ยวข้องอาจปรากฏขึ้น

• การแทนที่นิพจน์ทางด้านซ้ายและด้านขวาของสมการด้วยนิพจน์ที่เท่ากัน

เราได้พิสูจน์แล้วว่าการเปลี่ยนแปลงนี้จะเทียบเท่าหากการใช้งานไม่เปลี่ยน OD แล้วถ้า DL เปลี่ยนไปจะเกิดอะไรขึ้น? การทำให้ ODZ แคบลงอาจนำไปสู่การสูญเสียรากซึ่งจะกล่าวถึงรายละเอียดเพิ่มเติมในย่อหน้าถัดไป และด้วยการขยายตัวของ ODZ รากภายนอกอาจปรากฏขึ้น ไม่ใช่เรื่องยากที่จะให้เหตุผลเรื่องนี้ ให้เรานำเสนอเหตุผลที่เกี่ยวข้อง

ปล่อยให้นิพจน์ C(x) มีค่าเท่ากันกับนิพจน์ A(x) และ OD สำหรับสมการ C(x)=B(x) นั้นกว้างกว่า OD สำหรับสมการ A(x)=B (x) ขอให้เราพิสูจน์ว่าสมการ C(x)=B(x) เป็นผลมาจากสมการ A(x)=B(x) และในบรรดารากของสมการ C(x)=B(x) อาจมี เป็นรากที่ต่างจากสมการ A( x)=B(x)

ให้ q เป็นรากของสมการ A(x)=B(x) . จากนั้น A(q)=B(q) คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง เนื่องจาก ODZ สำหรับสมการ C(x)=B(x) กว้างกว่า ODZ สำหรับสมการ A(x)=B(x) ดังนั้นนิพจน์ C(x) จึงถูกกำหนดไว้ที่ x=q จากนั้นเมื่อคำนึงถึงความเท่าเทียมกันที่เหมือนกันของนิพจน์ C(x) และ A(x) เราจะสรุปได้ว่า C(q)=A(q) . จากความเท่าเทียมกัน C(q)=A(q) และ A(q)=B(q) เนื่องจากคุณสมบัติการส่งผ่าน ความเท่าเทียมกัน C(q)=B(q) ตามมา จากความเท่าเทียมกันนี้ q คือรากของสมการ C(x)=B(x) . สิ่งนี้พิสูจน์ว่าภายใต้เงื่อนไขที่ระบุ สมการ C(x)=B(x) เป็นผลมาจากสมการ A(x)=B(x)

ยังคงต้องพิสูจน์ว่าสมการ C(x)=B(x) สามารถมีรากที่แตกต่างจากรากของสมการ A(x)=B(x) ให้เราพิสูจน์ว่ารากใดๆ ของสมการ C(x)=B(x) จาก ODZ สำหรับสมการ A(x)=B(x) คือรากของสมการ A(x)=B(x) เส้นทาง p คือรากของสมการ C(x)=B(x) ที่เป็นของ ODZ สำหรับสมการ A(x)=B(x) ดังนั้น C(p)=B(p) คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง เนื่องจาก p อยู่ใน ODZ สำหรับสมการ A(x)=B(x) ดังนั้นนิพจน์ A(x) จึงถูกกำหนดไว้สำหรับ x=p จากนี้และจากความเท่าเทียมกันที่เหมือนกันของนิพจน์ A(x) และ C(x) จะเป็นไปตามนั้น A(p)=C(p) . จากความเท่าเทียมกัน A(p)=C(p) และ C(p)=B(p) เนื่องจากคุณสมบัติการผ่านผ่าน จึงเป็นไปตามที่ A(p)=B(p) ซึ่งหมายความว่า p คือรากของ สมการ A(x)= B(x) . นี่พิสูจน์ว่ารากใดๆ ของสมการ C(x)=B(x) จาก ODZ สำหรับสมการ A(x)=B(x) คือรากของสมการ A(x)=B(x) กล่าวอีกนัยหนึ่ง บน ODZ สำหรับสมการ A(x)=B(x) ไม่สามารถมีรากของสมการ C(x)=B(x) ซึ่งเป็นรากที่ไม่เกี่ยวข้องสำหรับสมการ A(x)=B( x) แต่ตามเงื่อนไข ODZ สำหรับสมการ C(x)=B(x) จะกว้างกว่า ODZ สำหรับสมการ A(x)=B(x) และสิ่งนี้ทำให้มีตัวเลข r ที่เป็นของ ODZ สำหรับสมการ C(x)=B(x) อยู่ได้ และไม่ได้อยู่ใน ODZ สำหรับสมการ A(x)=B(x) ซึ่งเป็นราก ของสมการ C(x)=B(x) นั่นคือ สมการ C(x)=B(x) อาจมีรากที่ต่างจากสมการ A(x)=B(x) และสมการทั้งหมดจะอยู่ในเซตที่ ODZ สำหรับสมการ A (x)=B ถูกขยาย (x) เมื่อแทนที่นิพจน์ A(x) ในนั้นด้วยนิพจน์ที่เท่ากัน C(x)

ดังนั้นการแทนที่นิพจน์ทางด้านซ้ายและด้านขวาของสมการด้วยนิพจน์ที่เท่ากันซึ่งเป็นผลมาจากการขยาย ODZ ในกรณีทั่วไปจะนำไปสู่สมการที่พิสูจน์ได้ (นั่นคือมันสามารถนำไปสู่การปรากฏตัวของสิ่งภายนอก) ราก) และเฉพาะบางกรณีเท่านั้นที่จะนำไปสู่สมการที่เทียบเท่า (ในกรณีที่สมการผลลัพธ์ไม่มีรากที่แตกต่างจากสมการดั้งเดิม)

ให้เรายกตัวอย่างการดำเนินการแปลงแยกวิเคราะห์ แทนที่นิพจน์ทางด้านซ้ายของสมการ เท่ากันกับนิพจน์ x·(x−1) นำไปสู่สมการ x·(x−1)=0 ในกรณีนี้ การขยายตัวของ ODZ เกิดขึ้น - เลข 0 จะถูกบวกเข้าไป สมการที่ได้จะมีราก 0 และ 1 สองราก และการแทนที่รากเหล่านี้เป็นสมการดั้งเดิมแสดงว่า 0 เป็นรากที่ไม่เกี่ยวข้องสำหรับสมการดั้งเดิม และ 1 คือรากของสมการดั้งเดิม อันที่จริงการแทนที่ศูนย์ในสมการดั้งเดิมจะทำให้การแสดงออกไม่มีความหมาย เนื่องจากมีการหารด้วยศูนย์ และการแทนที่หนึ่งจะทำให้ได้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง ซึ่งเหมือนกับ 0=0

โปรดทราบว่าการเปลี่ยนแปลงที่คล้ายกันของสมการที่คล้ายกัน ในสมการ (x−1)·(x−2)=0 ซึ่งเป็นผลมาจากการที่ ODZ ขยายออกด้วย ไม่ได้นำไปสู่การปรากฏตัวของรากภายนอก แท้จริงแล้ว รากทั้งสองของสมการผลลัพธ์ (x−1)·(x−2)=0 - ตัวเลข 1 และ 2 เป็นรากของสมการดั้งเดิม ซึ่งง่ายต่อการตรวจสอบโดยการตรวจสอบด้วยการแทนที่ จากตัวอย่างเหล่านี้ เราต้องการเน้นย้ำอีกครั้งว่าการแทนที่นิพจน์ทางด้านซ้ายหรือด้านขวาของสมการด้วยนิพจน์ที่เท่ากันซึ่งจะขยาย ODZ ไม่จำเป็นต้องนำไปสู่การปรากฏตัวของรากที่ไม่เกี่ยวข้องเสมอไป แต่ก็สามารถนำไปสู่การปรากฏตัวได้เช่นกัน ดังนั้นหากการเปลี่ยนแปลงดังกล่าวเกิดขึ้นในกระบวนการแก้สมการก็จำเป็นต้องตรวจสอบเพื่อระบุและกรองรากที่ไม่เกี่ยวข้องออก

บ่อยครั้งที่ ODZ ของสมการสามารถขยายได้และรากที่ไม่เกี่ยวข้องอาจปรากฏขึ้นเนื่องจากการแทนที่ด้วยศูนย์ของความแตกต่างของนิพจน์ที่เหมือนกันหรือผลรวมของนิพจน์ที่มีเครื่องหมายตรงกันข้าม เนื่องจากการแทนที่ด้วยศูนย์ของผลิตภัณฑ์ด้วยปัจจัยศูนย์อย่างน้อยหนึ่งตัว เนื่องจากการลดเศษส่วนและเนื่องจากการใช้คุณสมบัติราก ยกกำลัง ลอการิทึม ฯลฯ

• การบวกจำนวนเดียวกันทั้งสองข้างของสมการ หรือการลบจำนวนเดียวกันออกจากทั้งสองข้างของสมการ

เราแสดงไปแล้วข้างต้นว่าการแปลงนี้เท่ากันเสมอ นั่นคือนำไปสู่สมการที่เทียบเท่ากัน ไปข้างหน้า.

• การเพิ่มนิพจน์เดียวกันลงทั้งสองด้านของสมการ หรือการลบนิพจน์เดียวกันออกจากทั้งสองด้านของสมการ

ในย่อหน้าก่อนหน้านี้ เราได้เพิ่มเงื่อนไขว่า ODZ สำหรับนิพจน์ที่กำลังเพิ่มหรือลบไม่ควรแคบกว่า ODZ สำหรับสมการที่กำลังแปลง เงื่อนไขนี้ทำให้การแปลงในคำถามเทียบเท่ากัน มีข้อโต้แย้งที่คล้ายกับที่ให้ไว้ในตอนต้นของย่อหน้านี้ของบทความเกี่ยวกับข้อเท็จจริงที่ว่าสมการที่เทียบเท่าเป็นกรณีพิเศษของสมการที่พิสูจน์แล้ว และความรู้เกี่ยวกับความเท่าเทียมกันของการแปลงนั้นมีประโยชน์มากกว่าความรู้ในเรื่องเดียวกัน การเปลี่ยนแปลง แต่จากมุมมองของข้อเท็จจริงที่ว่ามันนำไปสู่สมการที่พิสูจน์ได้

เป็นไปได้ไหมที่ผลจากการเพิ่มนิพจน์เดียวกันหรือลบนิพจน์เดียวกันจากทั้งสองด้านของสมการ จะได้สมการที่นอกเหนือจากรากทั้งหมดของสมการดั้งเดิมแล้ว จะมีรากอื่นอีกบ้าง ไม่เขาไม่สามารถ. ถ้า ODZ สำหรับนิพจน์ที่จะบวกหรือลบไม่แคบกว่า ODZ สำหรับสมการดั้งเดิม ผลจากการบวกหรือลบจะทำให้ได้สมการที่เทียบเท่ากัน หาก ODZ สำหรับนิพจน์ที่จะบวกหรือลบนั้นแคบกว่า ODZ สำหรับสมการดั้งเดิม สิ่งนี้สามารถนำไปสู่การสูญเสียราก และไม่ปรากฏลักษณะของรากที่ไม่เกี่ยวข้อง เราจะพูดถึงเรื่องนี้เพิ่มเติมในย่อหน้าถัดไป

• การถ่ายโอนคำศัพท์จากส่วนหนึ่งของสมการไปยังอีกส่วนหนึ่งโดยที่เครื่องหมายเปลี่ยนไปตรงกันข้าม

การแปลงสมการนี้จะเท่ากันเสมอ ดังนั้นจึงไม่มีเหตุผลที่จะพิจารณาว่าเป็นการเปลี่ยนแปลงที่นำไปสู่สมการ-ผลที่ตามมา ด้วยเหตุผลที่ระบุไว้ข้างต้น

• การคูณหรือหารทั้งสองข้างของสมการด้วยจำนวนเดียวกัน

ในย่อหน้าก่อนหน้านี้ เราได้พิสูจน์ว่าหากการคูณหรือการหารทั้งสองข้างของสมการทำได้ด้วยจำนวนที่ไม่เป็นศูนย์ นี่จะเป็นการแปลงสมการที่เท่ากัน ดังนั้นอีกครั้ง จึงไม่มีประโยชน์ที่จะพูดถึงเรื่องนี้ว่าเป็นการเปลี่ยนแปลงที่นำไปสู่สมการที่พิสูจน์ได้

แต่ที่นี่ควรให้ความสนใจกับการจองเกี่ยวกับผลต่างจากศูนย์ของจำนวนที่คูณหรือหารทั้งสองข้างของสมการ สำหรับการแบ่งเขตการจองนี้เข้าใจได้ - ตั้งแต่ชั้นประถมศึกษาเราเข้าใจเช่นนั้น คุณไม่สามารถหารด้วยศูนย์ได้. ทำไมข้อนี้สำหรับการคูณ? ลองคิดดูว่าการคูณทั้งสองข้างของสมการด้วยศูนย์จะทำให้เกิดผลลัพธ์อย่างไร เพื่อความชัดเจน ลองใช้สมการเฉพาะ เช่น 2 x+1=x+5 นี่คือสมการเชิงเส้นที่มีรากเดียวซึ่งก็คือเลข 4 ลองเขียนสมการที่จะได้รับโดยการคูณทั้งสองด้านของสมการด้วยศูนย์: (2 x+1) 0=(x+5) 0 แน่นอนว่ารากของสมการนี้คือตัวเลขใดๆ ก็ตาม เพราะเมื่อคุณแทนตัวเลขใดๆ ลงในสมการนี้แทนที่จะเป็นตัวแปร x คุณจะได้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง 0=0 นั่นคือในตัวอย่างของเรา การคูณทั้งสองข้างของสมการด้วยศูนย์ทำให้เกิดสมการที่พิสูจน์ได้ ซึ่งทำให้ปรากฏรากที่ไม่เกี่ยวข้องจำนวนอนันต์สำหรับสมการดั้งเดิม ยิ่งไปกว่านั้นเป็นที่น่าสังเกตว่าในกรณีนี้วิธีการคัดกรองรากภายนอกตามปกติไม่สามารถรับมือกับงานของพวกเขาได้ ซึ่งหมายความว่าการแปลงที่ทำไปไม่มีประโยชน์ในการแก้สมการดั้งเดิม และนี่คือสถานการณ์ทั่วไปสำหรับการเปลี่ยนแปลงที่กำลังพิจารณา นี่คือเหตุผลว่าทำไมการแปลง เช่น การคูณทั้งสองข้างของสมการด้วยศูนย์ จึงไม่ได้ใช้ในการแก้สมการ เรายังต้องดูการแปลงนี้และการแปลงอื่น ๆ ที่ไม่ควรใช้แก้สมการในย่อหน้าสุดท้าย

• การคูณหรือหารทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน

ในย่อหน้าก่อนหน้านี้ เราได้พิสูจน์ว่าการเปลี่ยนแปลงนี้เทียบเท่ากันหากตรงตามเงื่อนไขสองข้อ มาเตือนพวกเขากันเถอะ เงื่อนไขแรก: OD สำหรับนิพจน์นี้ไม่ควรแคบกว่า OD สำหรับสมการดั้งเดิม เงื่อนไขที่สอง: นิพจน์ที่ใช้ในการคูณหรือหารจะต้องไม่หายไปใน ODZ สำหรับสมการดั้งเดิม

เรามาเปลี่ยนเงื่อนไขแรกกัน นั่นคือ เราจะถือว่า OD สำหรับนิพจน์ที่เราวางแผนจะคูณหรือหารทั้งสองส่วนของสมการนั้นแคบกว่า OD สำหรับสมการดั้งเดิม จากผลของการเปลี่ยนแปลงดังกล่าว จะได้สมการโดยที่ ODZ จะแคบกว่า ODZ สำหรับสมการดั้งเดิม การเปลี่ยนแปลงดังกล่าวอาจนำไปสู่การสูญเสียรากได้เราจะพูดถึงสิ่งเหล่านี้ในย่อหน้าถัดไป

จะเกิดอะไรขึ้นถ้าเราลบเงื่อนไขที่สองเกี่ยวกับค่าที่ไม่ใช่ศูนย์ของนิพจน์ซึ่งทั้งสองข้างของสมการถูกคูณหรือหารด้วย ODZ สำหรับสมการดั้งเดิม

การหารทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน ซึ่งหายไปด้วย OD สำหรับสมการดั้งเดิม จะส่งผลให้สมการที่มี OD แคบกว่า OD สำหรับสมการดั้งเดิม อันที่จริงตัวเลขจะหลุดออกไป ทำให้นิพจน์ที่ใช้ในการหารกลายเป็นศูนย์ สิ่งนี้สามารถนำไปสู่การสูญเสียรากได้

แล้วการคูณทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน ซึ่งหายไปใน ODZ สำหรับสมการดั้งเดิมล่ะ จะเห็นได้ว่าเมื่อทั้งสองด้านของสมการ A(x)=B(x) คูณด้วยนิพจน์ C(x) โดยที่ ODZ ไม่ได้แคบกว่า ODZ สำหรับสมการดั้งเดิม และหายไปด้วย ODZ สำหรับสมการดั้งเดิม จะได้สมการมาด้วย ซึ่งนอกจากรากทั้งหมดของสมการ A(x)=B(x) แล้ว ยังสามารถมีรากอื่นได้อีกด้วย มาทำสิ่งนี้กันเถอะ โดยเฉพาะอย่างยิ่งเมื่อย่อหน้านี้เน้นไปที่การแปลงที่นำไปสู่สมการที่พิสูจน์แล้ว

ปล่อยให้นิพจน์ C(x) เป็นเช่นนั้น โดยที่ ODZ สำหรับมันไม่แคบกว่า ODZ สำหรับสมการ A(x)=B(x) และหายไปใน ODZ สำหรับสมการ A(x)=B(x ) . ให้เราพิสูจน์ว่าในกรณีนี้สมการ A(x)·C(x)=B(x)·C(x) เป็นผลมาจากสมการ A(x)=B(x)

ให้ q เป็นรากของสมการ A(x)=B(x) . จากนั้น A(q)=B(q) คือความเท่าเทียมกันเชิงตัวเลขที่แท้จริง เนื่องจาก ODZ สำหรับนิพจน์ C(x) ไม่ได้แคบกว่า ODZ สำหรับสมการ A(x)=B(x) ดังนั้นนิพจน์ C(x) จึงถูกกำหนดไว้ที่ x=q ซึ่งหมายความว่า C(q) เป็นจำนวนที่แน่นอน การคูณทั้งสองด้านของความเท่าเทียมกันของตัวเลขที่แท้จริงด้วยจำนวนใดๆ จะทำให้เกิดความเท่าเทียมกันของตัวเลขที่แท้จริง ดังนั้น A(q)·C(q)=B(q)·C(q) จึงเป็นความเท่าเทียมกันของตัวเลขที่แท้จริง นี่หมายความว่า q เป็นรากของสมการ A(x)·C(x)=B(x)·C(x) นี่พิสูจน์ว่ารากใดๆ ของสมการ A(x)=B(x) คือรากของสมการ A(x) C(x)=B(x) C(x) ซึ่งหมายความว่าสมการ A(x) C (x)=B(x)·C(x) เป็นผลมาจากสมการ A(x)=B(x)

โปรดทราบว่าภายใต้เงื่อนไขที่ระบุ สมการ A(x)·C(x)=B(x)·C(x) อาจมีรากที่แตกต่างจากสมการดั้งเดิม A(x)=B(x) เป็นตัวเลขทั้งหมดจาก ODZ สำหรับสมการดั้งเดิมที่เปลี่ยนนิพจน์ C(x) ให้เป็นศูนย์ (ตัวเลขทั้งหมดที่เปลี่ยนนิพจน์ C(x) ให้เป็นศูนย์คือรากของสมการ A(x) C(x)=B (x) C(x) เนื่องจากการแทนที่ลงในสมการที่ระบุให้ความเท่าเทียมกันทางตัวเลขที่ถูกต้อง 0=0 ) แต่ไม่ใช่รากของสมการ A(x)=B(x) สมการ A(x)=B(x) และ A(x)·C(x)=B(x)·C(x) ภายใต้เงื่อนไขที่กำหนดจะเท่ากันเมื่อตัวเลขทั้งหมดจาก ODZ สำหรับสมการ A(x )=B (x) ซึ่งทำให้นิพจน์ C(x) หายไป คือรากของสมการ A(x)=B(x)

ดังนั้น เมื่อคูณทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน ODZ ซึ่งไม่แคบกว่า ODZ สำหรับสมการดั้งเดิม และหายไปด้วย ODZ สำหรับสมการดั้งเดิม ในกรณีทั่วไปจะนำไปสู่สมการที่พิสูจน์ได้ว่า คือสามารถนำไปสู่การปรากฏตัวของรากต่างประเทศได้

ลองยกตัวอย่างเพื่อแสดง ลองใช้สมการ x+3=4 กัน รากเดียวของมันคือหมายเลข 1 ลองคูณทั้งสองข้างของสมการนี้ด้วยนิพจน์เดียวกัน ซึ่งจะหายไปด้วย ODZ สำหรับสมการดั้งเดิม ตัวอย่างเช่น ด้วย x·(x−1) นิพจน์นี้หายไปเมื่อ x=0 และ x=1 การคูณทั้งสองข้างของสมการด้วยนิพจน์นี้จะทำให้เราได้สมการ (x+3) x (x−1)=4 x (x−1). สมการผลลัพธ์มีสองราก: 1 และ 0 เลข 0 เป็นรากที่ไม่เกี่ยวข้องสำหรับสมการดั้งเดิมซึ่งปรากฏเป็นผลมาจากการแปลง

การเปลี่ยนแปลงที่อาจนำไปสู่การสูญเสียราก

การแปลงบางอย่างจากภายใต้เงื่อนไขบางประการอาจทำให้สูญเสียรากได้ ตัวอย่างเช่น เมื่อหารทั้งสองข้างของสมการ x·(x−2)=x−2 ด้วยนิพจน์เดียวกัน x−2 รากจะสูญหายไป อันที่จริง จากผลของการแปลงดังกล่าว จะได้สมการ x=1 มาจากรากเดียวซึ่งก็คือเลข 1 และสมการดั้งเดิมมีสองรากคือ 1 และ 2

มีความจำเป็นต้องเข้าใจอย่างชัดเจนเมื่อรากสูญเสียไปอันเป็นผลมาจากการเปลี่ยนแปลงเพื่อไม่ให้สูญเสียรากเมื่อแก้สมการ ลองคิดดูสิ

จากผลของการแปลงเหล่านี้ การสูญเสียรากสามารถเกิดขึ้นได้ก็ต่อเมื่อ ODZ สำหรับสมการที่ถูกแปลงกลายเป็นแคบกว่า ODZ สำหรับสมการดั้งเดิม

เพื่อพิสูจน์ข้อความนี้ จำเป็นต้องพิสูจน์สองประเด็น ขั้นแรกจำเป็นต้องพิสูจน์ว่าหากเป็นผลมาจากการแปลงสมการที่ระบุ ODZ แคบลงก็อาจเกิดการสูญเสียรากได้ และประการที่สอง มีความจำเป็นต้องพิสูจน์ว่าหากเป็นผลมาจากการแปลงเหล่านี้ รากจะหายไป ดังนั้น ODZ สำหรับสมการผลลัพธ์จะแคบกว่า ODZ สำหรับสมการดั้งเดิม

หาก ODZ สำหรับสมการที่ได้รับจากการแปลงนั้นแคบกว่า ODZ สำหรับสมการดั้งเดิม ดังนั้น ตามธรรมชาติแล้ว ไม่ใช่รากเดียวของสมการดั้งเดิมที่อยู่นอก ODZ สำหรับสมการผลลัพธ์ที่สามารถเป็นรากของสมการได้ ที่ได้รับจากการเปลี่ยนแปลง ซึ่งหมายความว่ารากเหล่านี้จะหายไปเมื่อย้ายจากสมการดั้งเดิมไปเป็นสมการที่ ODZ แคบกว่า ODZ สำหรับสมการดั้งเดิม

ตอนนี้กลับมาแล้ว ขอให้เราพิสูจน์ว่าหากเป็นผลมาจากการแปลงเหล่านี้ รากหายไป ดังนั้น ODZ สำหรับสมการผลลัพธ์จะแคบกว่า ODZ สำหรับสมการดั้งเดิม ซึ่งสามารถทำได้โดยวิธีตรงกันข้าม สมมติฐานที่ว่าอันเป็นผลมาจากการเปลี่ยนแปลงเหล่านี้ทำให้รากหายไป แต่ ODZ ไม่ได้ถูกจำกัดให้แคบลง ขัดแย้งกับข้อความที่พิสูจน์แล้วในย่อหน้าก่อนหน้า แท้จริงแล้ว จากข้อความเหล่านี้ ตามมาว่าหากเมื่อดำเนินการแปลงที่ระบุ ODZ ไม่ได้ถูกจำกัดให้แคบลง ก็จะได้สมการที่เทียบเท่าหรือสมการที่เป็นผล ซึ่งหมายความว่าการสูญเสียรากจะไม่เกิดขึ้น

ดังนั้นสาเหตุของการสูญเสียรากที่อาจเกิดขึ้นเมื่อทำการแปลงสมการขั้นพื้นฐานคือการทำให้ ODZ แคบลง ชัดเจนว่าเมื่อแก้สมการแล้วเราไม่ควรเสียรากไป โดยธรรมชาติแล้ว คำถามนี้เกิดขึ้น: “เราควรทำอย่างไรเพื่อหลีกเลี่ยงการสูญเสียรากเมื่อเปลี่ยนสมการ” เราจะตอบในย่อหน้าถัดไป ทีนี้เรามาดูรายการการแปลงสมการพื้นฐานของสมการเพื่อดูรายละเอียดเพิ่มเติมว่าการแปลงใดสามารถนำไปสู่การสูญเสียรากได้

• การแทนที่นิพจน์ทางด้านซ้ายและด้านขวาของสมการด้วยนิพจน์ที่เท่ากัน

หากคุณแทนที่นิพจน์ทางด้านซ้ายหรือขวาของสมการด้วยนิพจน์ที่เท่ากัน OD ซึ่งแคบกว่า OD สำหรับสมการดั้งเดิม สิ่งนี้จะนำไปสู่การทำให้ OD แคบลง และด้วยเหตุนี้ราก อาจจะหายไป บ่อยครั้งที่การแทนที่นิพจน์ทางด้านซ้ายหรือด้านขวาของสมการด้วยนิพจน์ที่เท่ากันซึ่งดำเนินการบนพื้นฐานของคุณสมบัติบางประการของรากกำลังลอการิทึมและสูตรตรีโกณมิติบางสูตรนำไปสู่การทำให้ ODZ แคบลงและด้วยเหตุนี้ ไปจนถึงการสูญเสียรากที่เป็นไปได้ ตัวอย่างเช่น การแทนที่นิพจน์ทางด้านซ้ายของสมการด้วยนิพจน์ที่เท่ากันจะทำให้ ODZ แคบลง และทำให้สูญเสียราก −16 ในทำนองเดียวกัน การแทนที่นิพจน์ทางด้านซ้ายของสมการด้วยนิพจน์ที่เท่ากันจะนำไปสู่สมการที่ ODZ แคบกว่า ODZ สำหรับสมการดั้งเดิม ซึ่งทำให้สูญเสียราก −3

• การบวกจำนวนเดียวกันทั้งสองข้างของสมการ หรือการลบจำนวนเดียวกันออกจากทั้งสองข้างของสมการ

การเปลี่ยนแปลงนี้เทียบเท่ากัน ดังนั้น รากจะไม่สูญหายระหว่างการใช้งาน

• การเพิ่มนิพจน์เดียวกันลงทั้งสองด้านของสมการ หรือการลบนิพจน์เดียวกันออกจากทั้งสองด้านของสมการ

หากคุณเพิ่มหรือลบนิพจน์ที่มี OD แคบกว่า OD สำหรับสมการดั้งเดิม สิ่งนี้จะทำให้ OD แคบลง และผลที่ตามมาคืออาจสูญเสียรากได้ มันคุ้มค่าที่จะคำนึงถึงสิ่งนี้ แต่ที่นี่เป็นที่น่าสังเกตว่าในทางปฏิบัติมักจำเป็นต้องใช้วิธีเพิ่มหรือลบนิพจน์ที่มีอยู่ในการบันทึกสมการดั้งเดิมซึ่งไม่นำไปสู่การเปลี่ยนแปลงใน ODZ และไม่ทำให้เกิดการสูญเสียราก

• การถ่ายโอนคำศัพท์จากส่วนหนึ่งของสมการไปยังอีกส่วนหนึ่งโดยที่เครื่องหมายเปลี่ยนไปตรงกันข้าม

การเปลี่ยนแปลงของสมการนี้เทียบเท่ากัน ดังนั้น จากการนำไปปฏิบัติ รากจึงไม่สูญหาย

• การคูณหรือหารทั้งสองข้างของสมการด้วยจำนวนเดียวกันที่ไม่ใช่ศูนย์

การเปลี่ยนแปลงนี้ยังเทียบเท่ากัน และด้วยเหตุนี้ การสูญเสียรากจึงไม่เกิดขึ้น

• การคูณหรือหารทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน

การเปลี่ยนแปลงนี้สามารถนำไปสู่การจำกัด OD ในสองกรณี: เมื่อ OD สำหรับนิพจน์ที่ใช้การคูณหรือการหารแคบกว่า OD สำหรับสมการดั้งเดิม และเมื่อการหารดำเนินการโดยนิพจน์ที่กลายเป็น ศูนย์บน OD สำหรับสมการดั้งเดิม โปรดทราบว่าในทางปฏิบัติ โดยทั่วไปไม่จำเป็นต้องใช้การคูณและหารทั้งสองข้างของสมการด้วยนิพจน์ที่มี VA ที่แคบกว่า แต่คุณต้องจัดการกับการหารด้วยนิพจน์ที่กลายเป็นศูนย์สำหรับสมการดั้งเดิม มีวิธีการที่ช่วยให้คุณสามารถรับมือกับการสูญเสียรากในระหว่างการแบ่งดังกล่าวได้เราจะพูดถึงเรื่องนี้ในย่อหน้าถัดไปของบทความนี้

จะหลีกเลี่ยงการสูญเสียรากได้อย่างไร?

หากคุณใช้เฉพาะการแปลงจากเป็นการแปลงสมการและในเวลาเดียวกันไม่อนุญาตให้จำกัด ODZ ให้แคบลง การสูญเสียรากจะไม่เกิดขึ้น

นี่หมายความว่าไม่สามารถทำการแปลงสมการอื่นได้อีกใช่หรือไม่ ไม่ มันไม่ได้หมายความว่าอย่างนั้น หากคุณคิดการเปลี่ยนแปลงอื่นๆ ของสมการและอธิบายได้ครบถ้วน นั่นคือ ระบุว่าเมื่อใดจะนำไปสู่สมการที่เทียบเท่า เมื่อใดจะเกิดสมการที่เป็นผลสืบเนื่อง และเมื่อใดที่สามารถนำไปสู่การสูญเสียรากได้ คุณก็สามารถนำมันมาใช้ได้ดี

เราควรละทิ้งการปฏิรูปที่จะจำกัด DPD ให้แคบลงโดยสิ้นเชิงหรือไม่? ไม่ควรทำอย่างนั้น. คงไม่เสียหายที่จะเก็บการแปลงคลังแสงของคุณซึ่งมีจำนวนจำกัดหลุดออกจาก ODZ สำหรับสมการดั้งเดิม เหตุใดจึงไม่ควรละทิ้งการเปลี่ยนแปลงดังกล่าว? เนื่องจากมีวิธีการหลีกเลี่ยงการสูญเสียรากในกรณีเช่นนี้ ประกอบด้วยการตรวจสอบตัวเลขที่หลุดออกจาก ODZ แยกต่างหากเพื่อดูว่ามีรากของสมการดั้งเดิมในหมู่ตัวเลขเหล่านั้นหรือไม่ คุณสามารถตรวจสอบได้โดยการแทนที่ตัวเลขเหล่านี้ลงในสมการดั้งเดิม พวกที่เมื่อแทนค่าแล้วให้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง ก็คือรากของสมการดั้งเดิม พวกเขาจะต้องรวมอยู่ในคำตอบ หลังจากการตรวจสอบดังกล่าว คุณสามารถดำเนินการเปลี่ยนแปลงตามแผนได้อย่างปลอดภัยโดยไม่ต้องกลัวว่าจะสูญเสียรากเหง้า

การแปลงทั่วไปโดยที่ ODZ สำหรับสมการจะถูกจำกัดให้เหลือตัวเลขหลายๆ ตัวคือการแบ่งทั้งสองด้านของสมการด้วยนิพจน์เดียวกัน ซึ่งจะกลายเป็นศูนย์ที่หลายจุดจาก ODZ สำหรับสมการดั้งเดิม การเปลี่ยนแปลงนี้เป็นพื้นฐานของวิธีการแก้ปัญหา สมการกลับกัน. แต่ยังใช้ในการแก้สมการประเภทอื่นด้วย ลองยกตัวอย่าง

สมการสามารถแก้ไขได้โดยการแนะนำตัวแปรใหม่ หากต้องการแนะนำตัวแปรใหม่ คุณต้องหารทั้งสองข้างของสมการด้วย 1+x แต่ด้วยการหารดังกล่าว อาจสูญเสียการรูต เนื่องจากแม้ว่า ODZ สำหรับนิพจน์ 1+x จะไม่แคบกว่า ODZ สำหรับสมการดั้งเดิม แต่นิพจน์ 1+x จะกลายเป็นศูนย์ที่ x=−1 และตัวเลขนี้ เป็นของ ODZ สำหรับสมการดั้งเดิม ซึ่งหมายความว่าราก −1 อาจหายไป เพื่อกำจัดการสูญเสียราก คุณควรตรวจสอบแยกกันว่า −1 เป็นรากของสมการดั้งเดิมหรือไม่ ในการทำเช่นนี้ คุณสามารถแทนที่ −1 ลงในสมการดั้งเดิมแล้วดูว่าคุณได้ความเท่าเทียมกันเท่าใด ในกรณีของเรา การทดแทนให้ความเท่าเทียมกัน ซึ่งเท่ากับ 4=0 ความเท่าเทียมกันนี้เป็นเท็จ ซึ่งหมายความว่า −1 ไม่ใช่รากของสมการดั้งเดิม หลังจากตรวจสอบแล้ว คุณสามารถหารสมการทั้งสองข้างตามที่ต้องการได้ 1 + x โดยไม่ต้องกลัวว่าจะสูญเสียราก

ในตอนท้ายของย่อหน้านี้ ให้เรากลับมาที่สมการจากย่อหน้าก่อนหน้าอีกครั้งและ การแปลงสมการเหล่านี้โดยอาศัยอัตลักษณ์และ นำไปสู่การตีบแคบของ ODZ และทำให้เกิดการสูญเสียราก ณ จุดนี้ เรากล่าวว่าเพื่อไม่ให้สูญเสียรากเหง้าของเรา เราต้องละทิ้งการปฏิรูปที่ทำให้ DZ แคบลง ซึ่งหมายความว่าจะต้องละทิ้งการเปลี่ยนแปลงเหล่านี้ แต่เราควรทำอย่างไร? เป็นไปได้ที่จะดำเนินการเปลี่ยนแปลงโดยไม่ขึ้นอยู่กับตัวตนและ เนื่องจาก ODZ ถูกจำกัดให้แคบลง และอยู่บนพื้นฐานของข้อมูลประจำตัวและ . อันเป็นผลมาจากการเปลี่ยนจากสมการเดิมมาเป็นสมการและ ไม่มีการจำกัด ODZ ซึ่งหมายความว่ารากจะไม่สูญหาย

ในส่วนนี้ เราทราบเป็นพิเศษว่าเมื่อแทนที่นิพจน์ด้วยนิพจน์ที่เหมือนกัน คุณต้องตรวจสอบให้แน่ใจอย่างระมัดระวังว่านิพจน์นั้นเหมือนกันทุกประการ ตัวอย่างเช่น ในสมการ เป็นไปไม่ได้ที่จะแทนที่นิพจน์ x+3 ด้วยนิพจน์เพื่อทำให้รูปลักษณ์ด้านซ้ายง่ายขึ้น เนื่องจากนิพจน์ x+3 และไม่เท่ากัน เนื่องจากค่าไม่ตรงกันที่ x+3<0 . В нашем примере такое преобразование приводит к потере корня. А в общем случае замена выражения не тождественно равным выражением приводит к уравнению, которое не позволяет получить решение исходного уравнения.

การแปลงสมการที่ไม่ควรใช้

การเปลี่ยนแปลงที่กล่าวถึงในบทความนี้มักจะเพียงพอต่อความต้องการในทางปฏิบัติ นั่นคือคุณไม่ควรกังวลกับการเปลี่ยนแปลงอื่น ๆ มากเกินไป ควรมุ่งเน้นไปที่การใช้ที่ถูกต้องของการเปลี่ยนแปลงที่พิสูจน์แล้วแล้ว

วรรณกรรม

1. มอร์ดโควิช เอ.จี.พีชคณิตและจุดเริ่มต้นของการวิเคราะห์ทางคณิตศาสตร์ ชั้นประถมศึกษาปีที่ 11 ใน 2 ชั่วโมง ตอนที่ 1 หนังสือเรียนสำหรับนักเรียนสถาบันการศึกษาทั่วไป (ระดับโปรไฟล์) / A. G. Mordkovich, P. V. Semenov - ฉบับที่ 2, ลบแล้ว. - อ.: Mnemosyne, 2551. - 287 หน้า: ป่วย. ไอ 978-5-346-01027-2.
2. พีชคณิตและจุดเริ่มต้นของการวิเคราะห์ทางคณิตศาสตร์ เกรด 10: หนังสือเรียน เพื่อการศึกษาทั่วไป สถาบัน: พื้นฐานและโปรไฟล์ ระดับ / [ย. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; แก้ไขโดย เอ.บี. ซิจเชนโก้. - ฉบับที่ 3 - อ.: การศึกษา, 2553.- 368 หน้า: ill.-ISBN 978-5-09-022771-1.

ฟัน. ฟันของสัตว์มีกระดูกสันหลังมีโครงสร้างและพัฒนาการคล้ายคลึงกันอย่างสิ้นเชิงกับเกล็ดสงบซึ่งปกคลุมผิวหนังทั้งหมดของปลาฉลาม เนื่องจากช่องปากทั้งหมดและช่องคอหอยบางส่วนมีเยื่อบุผิวชั้นนอก (Ectodermal Epithelium) ซึ่งเป็นพลาคอยด์ทั่วไป... ...

วัณโรคปอด- วัณโรคปอด สารบัญ: I. พยาธิวิทยากายวิภาคศาสตร์.............110 II. การจำแนกประเภทของวัณโรคปอด.... 124 III. คลินิก.............128 IV. การวินิจฉัย..............160 V. การพยากรณ์โรค...................... .......... 190 วี. การรักษา … สารานุกรมการแพทย์ที่ยิ่งใหญ่

พิษ- พิษ การเป็นพิษหมายถึง "ความผิดปกติของการทำงานของสัตว์" สิ่งมีชีวิตที่เกิดจากสารออกฤทธิ์ภายนอกหรือภายนอกทางเคมีหรือทางกายภาพและทางเคมีซึ่งมีสิ่งแปลกปลอมในด้านคุณภาพ ปริมาณ หรือความเข้มข้น... ... สารานุกรมการแพทย์ที่ยิ่งใหญ่

แบคทีเรียก้อนพืชตระกูลถั่ว- ข้อมูลทางบรรพชีวินวิทยาระบุว่าพืชตระกูลถั่วที่เก่าแก่ที่สุดที่มีปมเป็นพืชบางชนิดที่อยู่ในกลุ่ม Eucaesalpinioideae. ในพืชตระกูลถั่วในปัจจุบัน พบว่ามีก้อน... สารานุกรมชีวภาพ

รายชื่อตอนของซีรีย์อนิเมชั่น "Luntik"- บทความนี้ไม่มีลิงก์ไปยังแหล่งข้อมูล ข้อมูลจะต้องสามารถตรวจสอบได้ มิฉะนั้นอาจถูกซักถามและลบทิ้ง คุณสามารถ... วิกิพีเดีย

พืชและสิ่งแวดล้อม- ชีวิตของพืชก็เหมือนกับสิ่งมีชีวิตอื่น ๆ ที่เป็นกระบวนการที่ซับซ้อนซึ่งสัมพันธ์กัน สิ่งที่สำคัญที่สุดดังที่ทราบกันดีคือการแลกเปลี่ยนสารกับสิ่งแวดล้อม สิ่งแวดล้อมเป็นแหล่งกำเนิด... ... สารานุกรมชีวภาพ

รายชื่อตอนของซีรีส์ "ลุนติค"- บทความหลัก: การผจญภัยของ Luntik และเพื่อน ๆ ของเขา สารบัญ 1 จำนวนตอนที่ 2 รายชื่อตอนของซีรีส์การ์ตูน Luntik และเพื่อน ๆ ของเขา ... Wikipedia

โรคไม้ผล- ต้องขอบคุณการดูแลของมนุษย์อย่างต่อเนื่อง ต้นไม้ผลไม้ควรจะมีอายุมากกว่าญาติที่ไม่ได้รับการปลูกฝัง หากไม่ใช่เพราะอิทธิพลที่ขัดขวางเงื่อนไขต่างๆ ของวัฒนธรรมเอง กล่าวคือ ความต้องการที่เราสร้างขึ้น... ...

การตัดโค่นป่า- การเก็บเกี่ยวป่าไม้หรือการสกัดรายได้จากป่าในรูปของไม้และเปลือกไม้ทำได้ 2 วิธี คือ การขุดหรือถอนต้นไม้ทั้งต้น คือ ลำต้นพร้อมราก หรือแยกเป็นบางส่วน โค่นก่อน หรือถอนออก จาก... ... พจนานุกรมสารานุกรม F.A. บร็อคเฮาส์ และ ไอ.เอ. เอโฟรน

กรอช- (ภาษาโปแลนด์ grosz จากภาษาเยอรมัน Groschen จากภาษาละติน Grossus (dēnārius) “เดนาเรียสหนา”) เหรียญของประเทศและช่วงเวลาต่างๆ สารบัญ 1 การปรากฏตัวของเพนนี ... Wikipedia

เหรียญสหรัฐ- 20 ดอลลาร์ Saint Gaudens เหรียญสหรัฐที่สวยที่สุดและแพงที่สุด เหรียญสหรัฐคือเหรียญที่สร้างเสร็จที่โรงกษาปณ์สหรัฐ ผลิตตั้งแต่ปี พ.ศ. 2335... วิกิพีเดีย

หนังสือ

• สาเหตุหลักของผมร่วงในผู้หญิง Alexey Michman ผู้หญิงหกในสิบคนต้องทนทุกข์ทรมานจากปัญหาผมร่วงในช่วงใดช่วงหนึ่งของชีวิต ผมร่วงเกิดได้จากหลายสาเหตุ เช่น กรรมพันธุ์ การเปลี่ยนแปลงของฮอร์โมนใน...

การสูญเสียรากและรากภายนอกเมื่อแก้สมการ

สถาบันการศึกษาเทศบาล "โรงเรียนมัธยมหมายเลข 2 พร้อมการศึกษาเชิงลึกของแต่ละวิชา" ในเมือง Vsevolozhsk งานวิจัยจัดทำโดยนักเรียนเกรด 11 B: Vasilyev Vasily ผู้จัดการโครงการ: Egorova Lyudmila Alekseevna

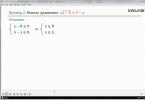
สมการก่อนอื่น เรามาดูวิธีต่างๆ ในการแก้สมการ sinx+cosx =- 1 กัน

วิธีแก้ปัญหาหมายเลข 1 sinx+cosx =-1 i Y x 0 1 sin(x+)=- 1 sin(x+)=- x+ =- +2 x+ = +2 + x=- +2 x= +2 คำตอบ: + 2

คำตอบที่ 2 sinx+cosx =- คำตอบที่ 1: +2 y x 0 1 2sin cos + - + + = 0 sin cos + = 0 cos (cos + sin)= 0 cos =0 cos + sin =1 = + m tg =-1 = + ม =- + x=- +2 x= +2

วิธีแก้ปัญหาหมายเลข 3 I y x 0 1 sinx+cosx =- 1 2 = x= x+ x sin2x=0 2x= x=

sinx+cosx =-1 วิธีแก้ปัญหาหมายเลข 4 i y x 0 1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n คำตอบ: - + 2 n

มาเปรียบเทียบวิธีแก้ปัญหากันดีกว่า วิธีแก้ปัญหาที่ถูกต้อง ลองคิดดูว่าในกรณีใดบ้างที่รากที่ไม่เกี่ยวข้องอาจปรากฏขึ้นและเหตุใด คำตอบที่ 2: +2 หมายเลข 3 คำตอบ: หมายเลข 4 คำตอบ: + 2 n หมายเลข 1 คำตอบ: +2

การตรวจสอบวิธีแก้ปัญหา จำเป็นต้องตรวจสอบหรือไม่? ฉันควรตรวจสอบรากเผื่อไว้เพื่อความปลอดภัยหรือไม่? แน่นอนว่าสิ่งนี้มีประโยชน์เมื่อทดแทนได้ง่าย แต่นักคณิตศาสตร์เป็นคนมีเหตุผลและไม่ทำสิ่งที่ไม่จำเป็น มาดูกรณีต่างๆ กัน และจำไว้ว่าเมื่อใดที่จำเป็นต้องมีการยืนยันจริงๆ

1. สูตรสำเร็จรูปที่ง่ายที่สุด c osx =a x=a =a s inx =a t gx =a ในกรณีที่หารากโดยใช้สูตรสำเร็จรูปที่ง่ายที่สุด ก็ไม่จำเป็นต้องตรวจสอบ อย่างไรก็ตาม เมื่อใช้สูตรดังกล่าว คุณควรจำเงื่อนไขที่สามารถใช้ได้ ตัวอย่างเช่น สูตร = สามารถใช้ได้ภายใต้เงื่อนไข a 0, -4ac 0 และคำตอบ x= arccos2+2 สำหรับสมการ cosx =2 ถือเป็นข้อผิดพลาดขั้นต้น เนื่องจากสูตร x= arccos a +2 สามารถทำได้เพียง ใช้สำหรับรากของสมการ cosx =a โดยที่ | ก | 1

2. การแปลง บ่อยครั้งที่เมื่อแก้สมการ คุณจะต้องทำการแปลงหลายอย่าง หากสมการถูกแทนที่ด้วยสมการใหม่ที่มีรากของสมการก่อนหน้าทั้งหมดและถูกแปลงเพื่อไม่ให้สูญเสียหรือได้มาซึ่งรากเกิดขึ้น สมการดังกล่าวจะเรียกว่าสมมูล 1. เมื่อถ่ายโอนส่วนประกอบของสมการจากส่วนหนึ่งไปยังอีกส่วนหนึ่ง 2. เมื่อบวกเลขเท่ากันทั้งสองข้าง 3. เมื่อทั้งสองข้างของสมการคูณด้วยจำนวนที่ไม่เป็นศูนย์อันเดียวกัน 4. เมื่อนำอัตลักษณ์ที่เป็นจริงมาใช้กับเซตของจำนวนจริงทั้งหมด อย่างไรก็ตาม ไม่จำเป็นต้องมีการตรวจสอบ!

อย่างไรก็ตาม ไม่ใช่ทุกสมการจะสามารถแก้ไขได้ด้วยการแปลงที่เท่ากัน บ่อยครั้งที่จำเป็นต้องใช้การแปลงที่ไม่เท่ากัน บ่อยครั้งที่การแปลงดังกล่าวขึ้นอยู่กับการใช้สูตรที่ไม่ถูกต้องกับค่าจริงทั้งหมด ในกรณีนี้ ขอบเขตของคำจำกัดความของสมการจะเปลี่ยนไป พบข้อผิดพลาดนี้ในโซลูชัน #4 ลองดูที่ข้อผิดพลาด แต่ก่อนอื่นเรามาดูวิธีแก้ปัญหาหมายเลข 4 อีกครั้ง sinx+cosx=-1 + =-1 2tg +1- =-1- 2tg =-2 =- + n x = - + 2 n ข้อผิดพลาดอยู่ในสูตร sin2x= สูตรนี้สามารถใช้ได้ แต่คุณควรตรวจสอบเพิ่มเติม ว่ารากเป็นตัวเลขของรูปแบบ + ซึ่งไม่ได้กำหนด tg หรือไม่ ตอนนี้เห็นได้ชัดว่าวิธีแก้ปัญหาคือการสูญเสียราก มาดูกันจนจบเลย

วิธีแก้ปัญหาหมายเลข 4 i y x 0 1 ลองตรวจสอบตัวเลข = + n โดยการแทนที่: x= + 2 n sin(+ 2 n)+ cos (+ 2 n)=sin + cos =0+(-1)=- 1 ดังนั้น x= +2 n คือรากของสมการ คำตอบ: +2 sinx+cosx =-1 + =- 1 2tg +1- =-1- 2tg =- 2 =- + n x= - + 2 n

เราพิจารณาวิธีหนึ่งในการสูญเสียราก มีหลายวิธีในคณิตศาสตร์ ดังนั้นคุณต้องแก้อย่างระมัดระวังโดยจดจำกฎทั้งหมด เช่นเดียวกับที่คุณสามารถสูญเสียรากของสมการได้ คุณยังสามารถหารากเพิ่มเติมในระหว่างการแก้สมการได้อีกด้วย ลองพิจารณาวิธีแก้ปัญหาหมายเลข 3 ที่เกิดข้อผิดพลาดดังกล่าว

โซลูชัน # 3 ฉัน x 0 1 2 2 และรูทพิเศษ! รากที่ไม่เกี่ยวข้องอาจปรากฏขึ้นเมื่อทั้งสองข้างของสมการกำลังสอง ในกรณีนี้จำเป็นต้องตรวจสอบ สำหรับ n=2k เรามี sin k+cos k=-1; cos k=-1 สำหรับ k=2m-1 จากนั้น n=2(2m+1)=4m+2 , x= = +2 m คำตอบ: +2 สำหรับ n=2k+1 เรามี sin +cos =- 1 บาป(+ k)+ cos (+ k)=- 1 cos k-sin k=- 1 cos k=-1 โดยที่ k=2m+1 n=2(2m+1)+ 1=2m+3 x= ( 4ม.+3)= +2 ม.=- +2 ซินx+คอสx =- 1 = x= x+ x บาป2x=0 2x= x=

ดังนั้นเราจึงพิจารณากรณีที่เป็นไปได้สองสามกรณี ซึ่งมีจำนวนมาก พยายามอย่าเสียเวลาและทำผิดพลาดโง่ ๆ

วิธีการพื้นฐานในการแก้สมการ

คำตอบของสมการคืออะไร?

การเปลี่ยนแปลงที่เหมือนกัน ขั้นพื้นฐาน

ประเภทของการเปลี่ยนแปลงอัตลักษณ์

รากต่างประเทศ การสูญเสียราก

การแก้สมการ เป็นกระบวนการที่ประกอบด้วยการแทนที่สมการที่กำหนดด้วยสมการอื่นที่เทียบเท่ากับสมการนั้นเป็นหลัก . การทดแทนนี้เรียกว่าการเปลี่ยนแปลงที่เหมือนกัน . การเปลี่ยนแปลงเอกลักษณ์หลักมีดังนี้:

1.

การแทนที่นิพจน์หนึ่งด้วยอีกนิพจน์หนึ่งที่เท่ากัน ตัวอย่างเช่น สมการ (3 x+ 2 ) 2 = 15 x+ 10 สามารถแทนที่ได้ด้วยการเทียบเท่าต่อไปนี้:9 x 2 + 12 x+ 4 = 15 x+ 10 .

2.

การถ่ายโอนเงื่อนไขของสมการจากด้านหนึ่งไปอีกด้านหนึ่งด้วยเครื่องหมายย้อนกลับ ดังนั้นในสมการก่อนหน้านี้ เราสามารถโอนพจน์ทั้งหมดจากด้านขวาไปด้านซ้ายด้วยเครื่องหมาย "-" ได้: 9 x 2 + 12 x+ 4 – 15 เอ็กซ์ – 10 = 0 หลังจากนั้นเราจะได้:9 x 2 – 3 เอ็กซ์ – 6 = 0 .

3.

การคูณหรือหารทั้งสองข้างของสมการด้วยนิพจน์เดียวกัน (ตัวเลข) ที่ไม่ใช่ศูนย์ สิ่งนี้สำคัญมากเพราะว่าสมการใหม่อาจไม่เทียบเท่ากับสมการก่อนหน้าหากนิพจน์ที่เรากำลังคูณหรือหารด้วยอาจเท่ากับศูนย์

ตัวอย่าง สมการเอ็กซ์ – 1 = 0 มีรากเดียวx= 1.

คูณทั้งสองข้างด้วยเอ็กซ์ – 3 เราจะได้สมการ

( เอ็กซ์ – 1)( เอ็กซ์ – 3) = 0 ซึ่งมีสองราก:x= 1 และx = 3.

ค่าสุดท้ายไม่ใช่รากของสมการที่กำหนด

เอ็กซ์ – 1 = 0 นี่คือสิ่งที่เรียกว่ารากภายนอก .

ในทางกลับกัน ความแตกแยกสามารถนำไปสู่การสูญเสียราก . ดังนั้น

ในกรณีของเรา ถ้า (เอ็กซ์ – 1 )( เอ็กซ์ – 3 ) = 0 คือค่าเดิม

สมการแล้วก็รากx= 3 จะหายไปในดิวิชั่น

ทั้งสองด้านของสมการเอ็กซ์ – 3 .

ในสมการสุดท้าย (ข้อ 2) เราสามารถหารพจน์ทั้งหมดด้วย 3 (ไม่ใช่ศูนย์!) และสุดท้ายก็ได้:

3 x 2 – x – 2 = 0 .

สมการนี้เทียบเท่ากับสมการดั้งเดิม:

(3 x+ 2) 2 = 15 x+ 10 .

4.

สามารถยกกำลังทั้งสองข้างของสมการให้เป็นกำลังคี่ หรือแยกรากคี่ออกจากทั้งสองข้างของสมการ . ต้องจำไว้ว่า:

ก) การก่อสร้างในแม้แต่ปริญญา อาจทำให้เกิดเพื่อการได้มาซึ่งรากต่างประเทศ ;

ข)ผิด การสกัดแม้แต่รูต สามารถนำไปสู่การสูญเสียราก .

ตัวอย่าง. สมการที่ 7x = 35 มีรากเดียวx = 5 .

โดยการยกกำลังสองทั้งสองข้างของสมการนี้ เราจะได้

สมการ:

49 x 2 = 1225 .

มีสองราก:x = 5 และx = – 5. ค่าสุดท้าย

เป็นรากที่อยู่ภายนอก

ไม่ถูกต้อง หารากที่สองของทั้งคู่

ส่วนของสมการที่ 49x 2 = 1225 ผลลัพธ์ใน 7x = 35,

และเรากำลังสูญเสียรากของเราx = – 5.

ถูกต้อง การหาผลลัพธ์ของสแควร์รูท

สมการ: | 7x | = 35, ก จึงมี 2 กรณี คือ

1) 7 x = 35, แล้วx = 5 ; 2) – 7 x = 35, แล้วx = – 5 .

ดังนั้นเมื่อถูกต้อง กำลังแยกสี่เหลี่ยม

รากเราจะไม่สูญเสียรากของสมการ

แปลว่าอะไรขวา แยกรากออกไหม? นี่คือที่ที่เราพบกัน

ด้วยแนวคิดที่สำคัญมากรากเลขคณิต

(ซม. ).