Solar radiation

All surface processes globe, - whatever they are, - have solar energy as their source. Whether purely mechanical processes are being studied, chemical processes in air, water, soil, physiological processes, or anything else at all, the primary cause of all of them, without exception, turns out to be the Sun. In all these processes, only one of the transformations of the initial energy that this central luminary of our planetary system sends to the Earth in the form of its rays occurs. In comparison with this main source of energy consumed by the globe, its other sources: radiation from stars, the Earth’s own heat, various space processes, - all of them are infinitesimal quantities. Therefore, the question of the amount of energy penetrating the earth’s surface from the Sun is the main question of the entire physics of the globe - meteorology. All this science is nothing more than the study and calculation of the income and expenditure, assets and liabilities of the energy received by the Earth from the Sun. Under the term "solar radiation" and they usually understand the energy that the Sun emits and which, being intercepted by the globe, is on this latter the primary source - primum mobile - of all phenomena and processes of the inorganic and animal worlds. - If the earth’s surface were not protected from the direct action of solar rays by an air shell covering it with a thick layer up to several hundred kilometers thick, studying that part of solar radiation that falls to the Earth would be very simple. Having measured once only at a certain moment and in a certain place the intensity of S. radiation, we could then, using elementary simple formulas pre-calculate the amount of energy at any moment and at any point on the globe. The presence of an atmosphere, which has the property of absorbing the sun's rays to a very noticeable extent - and, moreover, different rays very differently - greatly complicates the matter. Let us first assume that the atmosphere is completely transparent and that, consequently, all the energy that is intercepted by the globe reaches the earth's surface. Since the amount of energy received by a given surface is proportional to the sine of the angle made by the incident beam of rays with the receiving surface, the main element determining the intensity of radiation on the earth's surface for any point will be the height of the Sun above the horizon; it will determine not only the voltage of the rays at a given moment, but also the entire amount of energy received by a unit of the earth's surface over a certain period of time can be calculated from the heights of the Sun. According to the change in the height of the Sun above the horizon during the day, the daily cycle of solar radiation will be very simple. From the moment of sunrise, radiation increases rapidly as the star rises above the horizon; then, having reached a fairly significant value, it begins to change more slowly until it reaches a maximum around noon. After noon, the radiation curve drops completely symmetrically, first slowly, then very quickly towards sunset. Since with a change in the latitude of a place, the midday heights of the Sun and the length of the day will change for the same day, the amount of energy received during the day depends on the latitude of the place. The amount of energy received from the source by a given surface will then be inversely proportional to the squares of the distance of this surface from the source. Therefore, the annual course of solar radiation for the same place will be determined not only by the midday altitudes of the Sun and the length of the day, which vary depending on the time of year, but also by the distance of the Earth from the Sun. At the equator, the length of day and night is the same throughout the year; the amount of energy received by a unit of the earth's surface per day will be greatest here at the equinoxes, when the midday Sun is at the zenith of the place, least at the solstices, when the heights of the Sun at noon decrease to 66 ° 33 ". Since, in addition, the distance of the Earth from the Sun at perihelion and aphelion are not the same, then in the annual course of radiation there will be two minima of unequal magnitude at the solstices and two maxima at the equinoxes. June minimum corresponding greatest distance Earth from the Sun, will be more significant than December, falling on closest distance between the Sun and Earth. One might, accordingly, think that the amount of energy received by the Earth from the September to March equinox will be greater than that received from the March to September equinox. However, this is not so: the greater distance of the Earth from the Sun at aphelion (March - September) is balanced by its greater duration (from the March to the September equinox - 186 days), while the other half of the year, corresponding to a smaller distance between the Earth and the Sun, is shorter (between September and March equinoxes - 179 days). The amounts of energy received by the Earth in both half-years thus turn out to be close to equal. As you move northward from the equator, it is easy to see that the December minimum will deepen more and more as the midday heights of the Sun and the length of the day decrease, and the June minimum will gradually become less and less noticeable; the maxima from the moments of the equinox will move closer to each other until they merge into one common one, occurring in June. It turns out; that according to calculations, the amount of energy received on a summer day by a unit of the Earth’s surface per day will increase with distance from the equator; this is, however, completely understandable, since the length of the summer day increases with distance from the equator. Finally, at the pole, where the Sun remains above the horizon for six whole months, the amount of energy received by a unit of the earth's surface on a summer day will be greatest, since the Sun shines here all 24 hours. Curve of the annual cycle of S. radiation from the moment spring equinox will here rapidly increase until the summer solstice and then fall just as quickly as the autumn equinox approaches. The same thing, only with the opposite arrangement of maxima and minima, will take place in the annual cycle for the southern hemisphere. If, now, from the assumption made about the complete transparency of the atmosphere for solar rays we move to reality, then from observations it turns out that only a certain part of the energy that the rays bring to the limits of the atmosphere reaches the earth's surface; the rest is absorbed by the atmosphere itself. If we denote by 1 the entire amount of energy brought by the sun's rays, then only in the best case will a portion not exceeding 0.8 reach the earth's surface. It is generally accepted to call the ratio of the amount of energy that reaches the earth's surface to the amount that actually falls within the atmosphere coefficient of atmospheric transparency. The amount of energy absorbed by the atmosphere will depend on the mass of air passed by the beam; and this latter will be greater the longer the path traveled by the rays in the atmosphere and the denser the layers of air passed through. Consequently, the absorption of rays by the atmosphere will be greater, the lower the height of the Sun above the horizon. The mass of air passed by the rays can be calculated using Lambert's formula:

e = √h 2 + 2rh + r 2 Cos 2 z - rCosz,

Where e- the length of the path traversed by a solar ray in the atmosphere, h- height of the atmosphere, which can be taken as a unit, r- length of the radius of the globe and z- zenith distance of the Sun. When the mass of air encountered by the ray, or - which is the same thing - the length of its path, is known, the number of rays reaching the surface of the Earth is determined by Bouguer's law, according to which "for a medium with a known transparency coefficient, the amount of energy passed through it decrease in a geometric progression, while the masses of the medium traversed by the ray increase in an arithmetic progression.” If we denote by i- the amount of energy at the surface of the Earth, through J- the same amount at the limit of the atmosphere, d- atmospheric transparency coefficient and e- mass of the atmosphere, then, according to Bouguer’s law

i = Jp e

Based on this law, knowing R, it is possible to calculate what the course of S. radiation will be in the presence of the atmosphere. At p- 0.75, - a value close to that given by observations, with the highest air transparency, the dotted curves in figure 1 give an idea of ​​​​the changes that will occur in the annual course of solar radiation under the influence of the atmosphere.

Direct measurements show, however, that in reality the phenomenon is even more complex. There is always a certain amount of water vapor in the atmosphere, which strongly absorbs the sun's rays. The amount of vapor in a given volume or mass of air is a variable quantity, depending on the temperature and the degree of saturation of the air. Therefore, it is very difficult to pre-calculate the effect of vapor on the absorption of solar energy in the atmosphere. Observations by Savelyev in Kiev, Krova in Montpellier, Colley and Myshkin in Petrovsko-Razumovsky, near Moscow, significantly illuminated the influence of this factor on solar radiation and showed that only on clear, cloudless winter days, when the amount of vapor in the atmosphere is very small, the daily curve the course of radiation approaches its theoretical form (curve aa"a in fig. 2. On summer days, a secondary minimum appears on the same curve around noon (curve bb"b), due to the fact that as the temperature increases towards noon, due to evaporation, the amount of vapor in the air also increases; absorption of rays by the atmosphere also increases with increasing vapor; As a result, the curve falls by noon.

The greatest amount of energy is obtained by the earth's surface on a clear spring day (curve ss"s); but here, too, a secondary low around noon is clearly visible. Something similar is obtained in the annual course of radiation according to direct observations in Kyiv. The annual cycle curve, rapidly increasing from winter to spring and summer, reaches its maximum not during the solstice, but in the month of May, after which it reveals a weak secondary minimum, depending on the increase in the amount of vapor in the air. A secondary, weaker maximum is observed in September. The amount of energy brought by the sun's rays to the earth's surface became the subject of precise changes only in Lately when methods for studying it were developed. During measurements, the energy of the sun's rays is absorbed by a blackened surface, usually covered with soot, and is thus converted into heat, which is spent on heating this surface; It is this heating that is actually measured. For complete certainty and comparability of all observations, the surface is always placed perpendicular to the rays incident on it. The measurement results are usually expressed by the number of small calories absorbed by the surface of 1 square meter. STM for 1 minute. Devices based on these principles, known as actinometers And pyrheliometers, have already been described in the appropriate places (see the corresponding article). Actinometric measurements always result in the intensity of radiation on a plate placed normal to the beam incident on it; Therefore, direct measurements give on a clear, sunny day values ​​larger than those shown in Fig. 2 dotted line; The data obtained from direct observations are depicted in the same Fig. solid lines. To obtain from these numbers the energy per unit of horizontal earth's surface, the observation results have to be multiplied by the sines of the heights of the Sun, which gives the dotted curves. Observations of solar radiation, carried out systematically or automatically recorded by the instruments themselves, made it possible to determine with sufficient probability the factors included in the equation expressing Bouguer’s law. For value J, that is, for the intensity of S. radiation at the limit of the atmosphere, usually called solar constant, the most probable values, according to the observations of Langley, Krov and Savelyev, range between 3.0 and 3.5 calories per cm 2 per minute; For p- atmospheric transparency coefficient, values ​​fluctuate between 0.8 and 0.5, depending on various circumstances, - most importantly from the content of vapors and dust in the air. Here, of course, we mean clear days. In cloudy weather these values ​​are very small; for this see also - Radiant heat. Measurements using actinometers and pyrheliometers are quite complex for ordinary weather stations. Therefore, observers of these latter, to form a rough idea of ​​the course of solar radiation, use heliographs (see). This device, strictly speaking, does not even measure the intensity of solar radiation, but only the duration of the sun's shine during the day. But even these data are important for science and life. In addition to the fact that the air itself absorbs the rays of the Sun, clouds floating in it, standing in the path of the rays, block their access to the earth's surface. It is these clouds that the heliograph records. Knowing from it the time when the Sun shone unhindered on the Earth, it is possible, although only with a very rough approximation, to form an idea of ​​solar radiation during the day.

G. Lyuboslavsky.

encyclopedic Dictionary F. Brockhaus and I.A. Efron. - S.-Pb.: Brockhaus-Efron. 1890-1907 .

See what “Solar radiation” is in other dictionaries:

Electromagnetic and corpuscular radiation of the Sun. Electromagnetic radiation covers the wavelength range from gamma radiation to radio waves, its energy maximum falls in the visible part of the spectrum. Corpuscular component of the solar... ... Big Encyclopedic Dictionary

solar radiation- The total flow of electromagnetic radiation emitted by the Sun and falling on the Earth... Dictionary of Geography

This term has other meanings, see Radiation (meanings). This article lacks links to sources of information. Information must be verifiable, otherwise it may be called into question... Wikipedia

Electromagnetic radiation emanating from the Sun and entering the earth's atmosphere. Solar radiation wavelengths are concentrated in the range from 0.17 to 4 µm with a max. at a wavelength of 0.475 µm. OK. 48% of solar radiation energy is visible... ... Geographical encyclopedia

Electromagnetic and corpuscular radiation of the Sun. Electromagnetic radiation covers the wavelength range from gamma radiation to radio waves, its energy maximum falls in the visible part of the spectrum. Corpuscular component of the solar... ... encyclopedic Dictionary

solar radiation- Saulės spinduliuotė statusas T sritis fizika atitikmenys: engl. solar radiation vok. Sonnenstrahlung, f rus. solar radiation, n; solar radiation, f; solar radiation, n pranc. rayonnement solaire, m … Fizikos terminų žodynas

For what reasons does it change when it reaches the earth's surface?

There are several such reasons.

It is known that the Earth rotates around the Sun not in a circle, but in an ellipse. As a result, the distance between the Earth and the Sun continuously changes throughout the year. The smallest distance occurs in January, when the Earth is at perihelion, and the greatest in July, when the Earth is at aphelion.

Thanks to this, everyone square centimeter a surface placed perpendicular to the sun's rays will receive 7 percent more solar radiation in January than in July. These periodic changes, repeated from year to year, are amenable to the most accurate calculation and do not require any measurements.

Further, depending on the height of the Sun above the horizon, the path length of a solar ray in the atmosphere changes very significantly. The lower the Sun is above the horizon, the less solar radiation should reach the earth's surface. Knowing the scattering and absorption properties of the so-called ideal atmosphere, that is, absolutely clean and dry, it is possible to calculate what the radiation at the earth’s surface would be in this case, and compare the radiation observed in natural conditions with it.

This comparison is made in table. 1, which provides values ​​for solar altitudes from 5 to 60 degrees.

As can be seen from the table, the presence of even an ideal atmosphere greatly affects solar radiation: the lower the height of the Sun, the more significantly the radiation is attenuated.

If there were no atmosphere at all, then at any height of the Sun we would always observe the same value - 1.88 calories. At a solar altitude of 60 degrees, the ideal atmosphere weakens solar radiation by 0.22 calories, while the real atmosphere weakens it by another 0.35 calories, mainly due to the content of water vapor and dust in the real atmosphere. In this case, only 1.31 calories reach the earth's surface. At a solar altitude of 30 degrees, the ideal atmosphere reduces radiation by 0.31 calories, and 1.11 calories reach the Earth. At a solar altitude of 5 degrees, the corresponding figures would be 0.73 and 0.39 calories. That's how much the atmosphere attenuates solar radiation!

In Fig. 5 this property of the atmosphere is especially clearly visible. Here the solar altitudes are plotted vertically, and the attenuation percentages are plotted horizontally.

The horizontal shading shows the attenuation of solar radiation in an ideal atmosphere, the oblique shading shows the attenuation caused by water vapor and dust contained in the real atmosphere, the vertical shading shows the amount of radiation that ultimately reaches the earth's surface.

From this graph it is clear, for example, that with average transparency of the atmosphere and with a solar altitude of 60 degrees, 70 percent of the radiation reaches the earth's surface, at 30 degrees - 60 percent, and at 5 degrees - only 20 percent.

Of course, in some cases, the transparency of the atmosphere may differ significantly from the average, especially towards its decrease.

The intensity of radiation incident on a horizontal surface also depends on the angle of incidence.

This is illustrated by Fig. 6. Let us assume that a sunbeam with cross section 1 square meter falls on plane ab below different angles. Pregnant I, when the beam falls perpendicularly, all the energy contained in the sun's beam will be distributed over an area of ​​1 square meter. Pregnant II the sun's rays fall at an angle of less than 90 degrees; in this case, a beam of solar rays of the same cross-section as in the first case falls on the area vg, which is greater ab; therefore, less energy will be needed per unit area.

Pregnant III the rays fall at an even smaller angle; the same radiant energy will be distributed over more larger area de, and per unit there is an even smaller value.

If the beam falls at an angle of 30 degrees, then the radiation per unit area will be 2 times less than with normal incidence; at an altitude of the Sun of 10 degrees it will be 6 times less, and at an altitude of 5 degrees it will be 12 times less.

This is why in winter, when the sun is at a low altitude, the influx of radiation is so small. On the one hand, it decreases because the sun's ray travels a long way in the atmosphere and loses a lot of energy along the way; on the other hand, the radiation itself falls at a small angle. Both of these reasons act in one direction, and the voltage of solar radiation compared to summer is completely negligible, and therefore the heating effect is insignificant; especially if you also take into account that winter days are short.

So, the main reasons that influence the amount of solar radiation reaching the earth's surface are the height of the Sun above the horizon and the angle of incidence of the radiation. Therefore, we should expect in advance significant changes in solar radiation depending on the latitude of the place.

Since systematic observations of solar radiation have now been carried out at many points and for a long time, it is interesting to see what the largest values ​​were obtained during this time under natural conditions.

Solar constant - 1.88 calories. This is the amount of radiation in the absence of an atmosphere. In an ideal atmosphere, in mid-latitudes, in summer time, in the afternoon hours the radiation would be equal to approximately 1.65 calories.

What do direct observations in natural conditions provide?

In table 2 shows a summary of the highest values ​​of solar radiation obtained from observations over a long period of time.

On the territory of the USSR, the highest measured value of radiation (for a low altitude above sea level) is 1.51 calories. The second column of numbers shows what percentage of radiation, compared to what would have been possible in the absence of an atmosphere, reached the earth's surface; It turns out that in the best case, only 80 percent reaches; The atmosphere does not allow 20 percent. In polar countries, this percentage is only slightly lower (70), which is explained by the high transparency of the atmosphere in the Arctic, especially considering that the height of the Sun during observations was significantly lower there than in points located further south.

It is quite natural that on the mountains and generally in higher layers of the atmosphere the intensity of solar radiation should increase, since the mass of the atmosphere traversed by the sun's ray decreases. At modern development aviation, one would expect that numerous measurements have been made on different heights, but, unfortunately, this is not the case: measurements at heights are single. This is explained by the complexity of actinometric measurements on balloons and especially on airplanes; In addition, the methodology for high-altitude radiation measurements has not yet been developed very much.

The intensity of sunlight that reaches the earth varies depending on the time of day, year, location and weather conditions. Total energy calculated per day or per year is called irradiation (or else “incoming solar radiation”) and shows how powerful the solar radiation was. Irradiation is measured in W*h/m2 per day, or other period.

The intensity of solar radiation in free space at a distance equal to the average distance between the Earth and the Sun is called the solar constant. Its value is 1353 W/m2. When passing through the atmosphere, sunlight is attenuated mainly due to the absorption of infrared radiation by water vapor, ultraviolet radiation— ozone and radiation scattering by atmospheric dust particles and aerosols. Index atmospheric influence the intensity of solar radiation reaching the earth's surface is called “air mass” (AM). AM is defined as the secant of the angle between the Sun and zenith.

Figure 1 shows the spectral distribution of solar radiation intensity in different conditions. The upper curve (AM0) corresponds to the solar spectrum outside the earth's atmosphere (for example, on board a spacecraft), i.e. at zero air mass. It is approximated by the distribution of the radiation intensity of a completely black body at a temperature of 5800 K. Curves AM1 and AM2 illustrate the spectral distribution of solar radiation on the Earth's surface when the Sun is at its zenith and at an angle between the Sun and the zenith of 60°, respectively. In this case, the total radiation power is approximately 925 and 691 W/m2, respectively. The average radiation intensity on Earth approximately coincides with the radiation intensity at AM = 1.5 (the Sun is at an angle of 45° to the horizon).

Near the Earth's surface, we can take the average value of solar radiation intensity as 635 W/m2. On a very clear sunny day, this value ranges from 950 W/m2 to 1220 W/m2. The average value is approximately 1000 W/m2. Example: Total radiation intensity in Zurich (47°30′N, 400 m above sea level) on a surface perpendicular to the radiation: May 1 12:00 1080 W/m 2 ; December 21 12:00 930 W/ m 2.

To simplify the calculation of solar energy arrival, it is usually expressed in hours of sunshine with an intensity of 1000 W/m2. Those. 1 hour corresponds to the arrival of solar radiation of 1000 W*h/m2. This roughly corresponds to the period when the sun shines in the summer in the middle of a sunny, cloudless day on a surface perpendicular to the sun's rays.

The arrival of solar radiation varies throughout the day and from place to place, especially in mountainous areas. Irradiation varies on average from 1000 kWh/m2 per year for Northern European countries, to 2000-2500 kWh/m2 per year for deserts. Weather conditions and the declination of the sun (which depends on the latitude of the area) also lead to differences in the arrival of solar radiation.

Example

The bright sun shines with an intensity of 1000 W/m2 on a surface perpendicular to the sun's rays. In 1 hour, 1 kWh of energy falls per 1 m2 (energy is equal to the product of power and time). Similarly, an average solar radiation arrival of 5 kWh/m2 during the day corresponds to 5 peak hours of sunshine per day. Do not confuse peak hours with actual daylight hours. During the day, the sun shines with different intensities, but in total it gives the same amount of energy as if it shone for 5 hours at maximum intensity. It is the peak hours of sunshine that are used in the calculations of solar energy installations.

In Russia, contrary to popular belief, there are many places where it is profitable to convert solar energy into electricity using. Below is a map of solar energy resources in Russia. As you can see, in most of Russia it can be successfully used in seasonal mode, and in areas with more than 2000 hours of sunshine per year - all year round. Naturally, in winter period energy production solar panels is significantly reduced, but still the cost of electricity from a solar power plant remains significantly lower than from a diesel or gasoline generator.

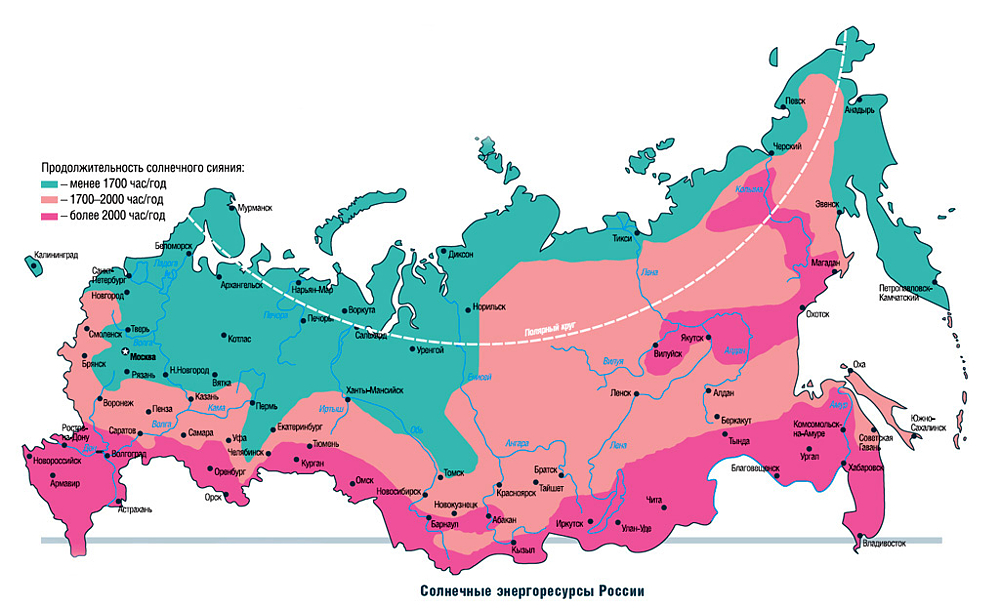
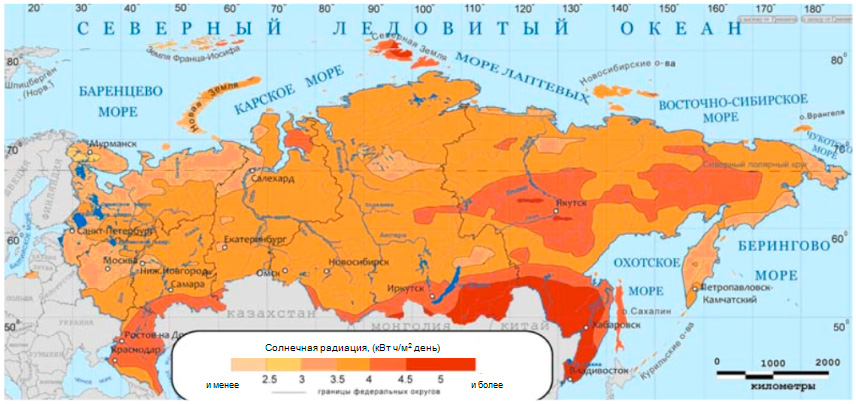
It is especially beneficial to use where there are no centralized electrical networks and energy supply is provided by diesel generators. And there are a lot of such areas in Russia.

Moreover, even where networks exist, the use of systems running in parallel with the network solar panels allows you to significantly reduce energy costs. With the current trend towards increasing tariffs of Russia's natural energy monopolies, installing solar panels is becoming a smart investment.