อสมการเรียกว่าเชิงเส้นด้านซ้ายและด้านขวาเป็นฟังก์ชันเชิงเส้นเทียบกับปริมาณที่ไม่ทราบ ซึ่งรวมถึงความไม่เท่าเทียมกัน เช่น:

2x-1-x+3; 7x0;

5 >4 - 6x 9- x< x + 5 .

1) อสมการที่เข้มงวด: ขวาน +b>0หรือ ขวาน+ข<0

2) อสมการที่ไม่เข้มงวด: ขวาน +b≤0หรือ ขวาน+ข≫ 0

มาวิเคราะห์งานนี้กัน- ด้านหนึ่งของสี่เหลี่ยมด้านขนานคือ 7 ซม. ด้านอีกด้านจะต้องยาวเป็นเท่าใดจึงทำให้เส้นรอบวงของสี่เหลี่ยมด้านขนานมากกว่า 44 ซม.

ปล่อยให้ด้านที่ต้องการเป็น เอ็กซ์ซม. ในกรณีนี้ เส้นรอบรูปของสี่เหลี่ยมด้านขนานจะแสดงด้วย (14 + 2x) ซม. อสมการ 14 + 2x > 44 เป็นแบบจำลองทางคณิตศาสตร์ของปัญหาเส้นรอบรูปของสี่เหลี่ยมด้านขนาน ถ้าเราแทนที่ตัวแปรในอสมการนี้ เอ็กซ์ตัวอย่างเช่น บนเลข 16 เราจะได้ค่าอสมการเชิงตัวเลขที่ถูกต้อง 14 + 32 > 44 ในกรณีนี้ พวกเขาบอกว่าเลข 16 เป็นวิธีแก้สมการของอสมการ 14 + 2x > 44

การแก้ปัญหาความไม่เท่าเทียมกันตั้งชื่อค่าของตัวแปรที่เปลี่ยนให้เป็นอสมการเชิงตัวเลขที่แท้จริง

ดังนั้นแต่ละตัวเลขคือ 15.1; 20;73 ทำหน้าที่เป็นคำตอบของอสมการ 14 + 2x > 44 แต่เช่น เลข 10 ไม่ใช่คำตอบของมัน

แก้ปัญหาความไม่เท่าเทียมกันหมายถึงการสร้างวิธีแก้ปัญหาทั้งหมดหรือเพื่อพิสูจน์ว่าไม่มีวิธีแก้ปัญหา

การกำหนดสูตรการแก้อสมการจะคล้ายกับการกำหนดรากของสมการ แต่ถึงกระนั้นก็ไม่ใช่ธรรมเนียมที่จะต้องระบุถึง "ต้นตอของความไม่เท่าเทียมกัน"

คุณสมบัติของความเท่าเทียมกันเชิงตัวเลขช่วยให้เราแก้สมการได้ ในทำนองเดียวกันคุณสมบัติของอสมการเชิงตัวเลขจะช่วยแก้อสมการได้

เมื่อแก้สมการ เราจะเปลี่ยนเป็นสมการอื่นที่มากกว่านั้น สมการง่ายๆแต่เทียบเท่ากับอันที่กำหนด คำตอบของความไม่เท่าเทียมกันก็พบได้ในลักษณะเดียวกัน เมื่อเปลี่ยนสมการให้เป็นสมการที่เทียบเท่ากัน พวกเขาใช้ทฤษฎีบทเกี่ยวกับการโอนเทอมจากด้านหนึ่งของสมการไปอีกด้านหนึ่ง และเกี่ยวกับการคูณทั้งสองข้างของสมการด้วยจำนวนที่ไม่เป็นศูนย์เดียวกัน เมื่อแก้อสมการ มีความแตกต่างอย่างมีนัยสำคัญระหว่างสมการกับสมการ ซึ่งอยู่ที่ความจริงที่ว่าการแก้สมการใดๆ สามารถตรวจสอบได้โดยการแทนที่สมการดั้งเดิม ในความไม่เท่าเทียมกัน วิธีนี้ขาดหายไป เนื่องจากเป็นไปไม่ได้ที่จะแทนที่วิธีแก้ปัญหาจำนวนนับไม่ถ้วนให้เป็นความไม่เท่าเทียมกันดั้งเดิม จึงมีแนวคิดที่สำคัญคือลูกศรเหล่านี้<=>เป็นเครื่องหมายของการแปลงที่เทียบเท่าหรือเทียบเท่า เรียกว่าการเปลี่ยนแปลง เทียบเท่า,หรือ เทียบเท่าหากไม่เปลี่ยนชุดการแก้ปัญหา

กฎที่คล้ายกันในการแก้ไขความไม่เท่าเทียมกัน

หากเราย้ายพจน์ใดๆ จากส่วนหนึ่งของความไม่เท่าเทียมกันไปยังอีกส่วนหนึ่ง โดยแทนที่เครื่องหมายด้วยคำที่ตรงกันข้าม เราจะได้ความไม่เท่าเทียมกันที่เทียบเท่ากับอันนี้

หากอสมการทั้งสองด้านคูณ (หาร) ด้วยจำนวนบวกเท่ากัน เราจะได้อสมการที่เทียบเท่ากับค่านี้

หากอสมการทั้งสองด้านถูกคูณ (หาร) ด้วยจำนวนลบเดียวกัน โดยแทนที่เครื่องหมายอสมการด้วยเครื่องหมายตรงข้าม เราจะได้อสมการที่เทียบเท่ากับค่าที่กำหนด

การใช้สิ่งเหล่านี้ กฎให้เราคำนวณอสมการต่อไปนี้

1) มาวิเคราะห์ความไม่เท่าเทียมกันกัน 2x - 5 > 9.

นี้ ความไม่เท่าเทียมกันเชิงเส้นเราจะหาแนวทางแก้ไขและหารือเกี่ยวกับแนวคิดพื้นฐาน

2x - 5 > 9<=>2x>14(5 ถูกย้ายไปทางซ้ายโดยมีเครื่องหมายตรงข้าม) จากนั้นเราหารทุกอย่างด้วย 2 แล้วเราก็ได้ x > 7- ให้เราพลอตเซตของคำตอบบนแกน x

เราได้รับลำแสงที่มีทิศทางบวก เราสังเกตชุดของการแก้ปัญหาทั้งในรูปแบบของความไม่เท่าเทียมกัน x > 7หรือในรูปของช่วง x(7; ∞) ข้อใดคือวิธีแก้ปัญหาเฉพาะของอสมการนี้? ตัวอย่างเช่น, x = 10เป็นวิธีแก้ปัญหาเฉพาะสำหรับอสมการนี้ x = 12- นี่เป็นวิธีแก้ปัญหาเฉพาะสำหรับอสมการนี้ด้วย

มีวิธีแก้ไขบางส่วนอยู่มากมาย แต่งานของเราคือค้นหาวิธีแก้ไขทั้งหมด และมักจะมีวิธีแก้ปัญหามากมายนับไม่ถ้วน

มาจัดเรียงกัน ตัวอย่างที่ 2:

2) แก้ปัญหาความไม่เท่าเทียมกัน 4a - 11 > ก + 13.

มาแก้กัน: กย้ายไปด้านหนึ่ง 11 ย้ายไปอีกด้านหนึ่ง เราได้ 3a< 24, и в результате после деления обеих частей на 3 ความไม่เท่าเทียมกันก็มีรูปแบบ ก<8 .

4a - 11 > ก + 13<=>3ก< 24 <=>ก< 8 .

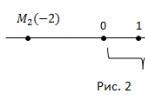
เราจะแสดงชุดด้วย ก< 8 แต่อยู่บนแกนแล้ว ก.

เราอาจเขียนคำตอบในรูปของอสมการ a< 8, либо ก(-∞;8), 8 เปิดไม่ติด

จำเป็นต้องเปรียบเทียบปริมาณและปริมาณเมื่อแก้ไขปัญหาเชิงปฏิบัติมาตั้งแต่สมัยโบราณ ในเวลาเดียวกัน คำว่ามากขึ้นและน้อยลง สูงขึ้นและต่ำลง เบาและหนักขึ้น เงียบขึ้นและดังขึ้น ถูกลงและมีราคาแพงขึ้น ฯลฯ ปรากฏขึ้น ซึ่งแสดงถึงผลลัพธ์ของการเปรียบเทียบปริมาณที่เป็นเนื้อเดียวกัน

แนวคิดเรื่องมากขึ้นเรื่อยๆ เกิดขึ้นจากการนับวัตถุ การวัด และการเปรียบเทียบปริมาณ ตัวอย่างเช่น นักคณิตศาสตร์ในยุคกรีกโบราณรู้ว่าด้านของสามเหลี่ยมใดๆ น้อยกว่าผลรวมของอีกสองด้านที่เหลือ และด้านที่ใหญ่กว่าของสามเหลี่ยมนั้นอยู่ตรงข้ามกับมุมที่ใหญ่กว่า ขณะคำนวณเส้นรอบวงของอาร์คิมิดีส พบว่าเส้นรอบวงของวงกลมใดๆ มีค่าเท่ากับสามเท่าของเส้นผ่านศูนย์กลาง โดยส่วนที่เกินนั้นน้อยกว่าหนึ่งในเจ็ดของเส้นผ่านศูนย์กลาง แต่มากกว่าสิบเจ็ดสิบเท่าของเส้นผ่านศูนย์กลาง

เขียนความสัมพันธ์ระหว่างตัวเลขและปริมาณเชิงสัญลักษณ์โดยใช้เครื่องหมาย > และ b บันทึกที่มีตัวเลขสองตัวเชื่อมต่อกันด้วยเครื่องหมายตัวใดตัวหนึ่ง: > (มากกว่า) คุณยังพบความไม่เท่าเทียมกันของตัวเลขในเกรดที่ต่ำกว่าอีกด้วย คุณรู้ว่าความไม่เท่าเทียมกันสามารถเป็นจริงได้ หรืออาจเป็นเท็จก็ได้ ตัวอย่างเช่น \(\frac(1)(2) > \frac(1)(3)\) คืออสมการเชิงตัวเลขที่ถูกต้อง 0.23 > 0.235 คืออสมการเชิงตัวเลขที่ไม่ถูกต้อง

ความไม่เท่าเทียมกันที่เกี่ยวข้องกับสิ่งไม่รู้อาจเป็นจริงสำหรับค่าบางอย่างของสิ่งที่ไม่รู้และเป็นเท็จสำหรับค่าอื่น ๆ ตัวอย่างเช่น อสมการ 2x+1>5 เป็นจริงสำหรับ x = 3 แต่เป็นเท็จสำหรับ x = -3 สำหรับความไม่เท่าเทียมกันกับสิ่งที่ไม่รู้จัก คุณสามารถกำหนดงานได้: แก้ไขความไม่เท่าเทียมกัน ปัญหาการแก้ไขอสมการในทางปฏิบัตินั้นถูกวางและแก้ไขไม่น้อยไปกว่าปัญหาการแก้สมการ ตัวอย่างเช่นมากมาย ปัญหาทางเศรษฐกิจเหลือเพียงการศึกษาและแก้ระบบอสมการเชิงเส้น ในหลายสาขาของคณิตศาสตร์ อสมการเป็นเรื่องธรรมดามากกว่าสมการ

อสมการบางอย่างทำหน้าที่เป็นวิธีช่วยเพียงวิธีเดียวในการพิสูจน์หรือพิสูจน์การมีอยู่ของวัตถุบางอย่าง เช่น รากของสมการ

อสมการเชิงตัวเลข

คุณสามารถเปรียบเทียบจำนวนเต็มได้หรือไม่? ทศนิยม- คุณรู้กฎการเปรียบเทียบหรือไม่? เศษส่วนสามัญมีตัวส่วนเท่ากันแต่มีตัวเศษต่างกัน ที่มีตัวเศษเท่ากันแต่มีตัวส่วนต่างกัน ที่นี่คุณจะได้เรียนรู้วิธีการเปรียบเทียบตัวเลขสองตัวใดๆ โดยการค้นหาสัญลักษณ์ของความแตกต่าง

การเปรียบเทียบตัวเลขมีการใช้กันอย่างแพร่หลายในทางปฏิบัติ ตัวอย่างเช่น นักเศรษฐศาสตร์เปรียบเทียบตัวบ่งชี้ที่วางแผนไว้กับตัวบ่งชี้ที่เกิดขึ้นจริง แพทย์จะเปรียบเทียบอุณหภูมิของผู้ป่วยกับอุณหภูมิปกติ ช่างกลึงจะเปรียบเทียบขนาดของชิ้นส่วนที่กลึงกับมาตรฐาน ในกรณีดังกล่าวทั้งหมด จะมีการเปรียบเทียบตัวเลขบางจำนวน จากการเปรียบเทียบตัวเลขทำให้เกิดความไม่เท่าเทียมกันทางตัวเลข

คำนิยาม.หมายเลข ก จำนวนมากขึ้น b ถ้าผลต่าง a-b เป็นบวก หมายเลข ก จำนวนน้อยลง b ถ้าผลต่าง a-b เป็นลบ

ถ้า a มากกว่า b แสดงว่า: a > b; ถ้า a น้อยกว่า b ก็เขียนว่า: a ดังนั้นความไม่เท่าเทียมกัน a > b หมายความว่าความแตกต่าง a - b เป็นบวก นั่นคือ a - b > 0. อสมการ a สำหรับตัวเลขสองตัวใดๆ a และ b จากความสัมพันธ์สามค่าต่อไปนี้ a > b, a = b, a ในการเปรียบเทียบตัวเลข a และ b หมายถึงการหาว่าเครื่องหมายใด >, = หรือ ทฤษฎีบท.ถ้า a > b และ b > c แล้ว a > c

ทฤษฎีบท.หากคุณบวกเลขเดียวกันทั้งสองด้านของอสมการ เครื่องหมายของอสมการจะไม่เปลี่ยนแปลง
ผลที่ตามมาคำใดๆ สามารถย้ายจากส่วนหนึ่งของความไม่เท่าเทียมกันไปยังอีกส่วนหนึ่งได้โดยการเปลี่ยนเครื่องหมายของคำนี้ไปเป็นคำตรงกันข้าม

ทฤษฎีบท.หากอสมการทั้งสองข้างคูณด้วยจำนวนบวกเท่ากัน สัญญาณของอสมการจะไม่เปลี่ยนแปลง หากอสมการทั้งสองข้างคูณด้วยจำนวนลบเท่ากัน สัญญาณของอสมการจะเปลี่ยนไปตรงกันข้าม
ผลที่ตามมาหากอสมการทั้งสองข้างหารด้วยจำนวนบวกเท่ากัน สัญญาณของอสมการจะไม่เปลี่ยนแปลง หากอสมการทั้งสองข้างหารด้วยจำนวนลบเท่ากัน สัญญาณของอสมการจะเปลี่ยนไปตรงกันข้าม

คุณรู้ว่าความเท่าเทียมกันของตัวเลขสามารถบวกและคูณทีละเทอมได้ ต่อไป คุณจะได้เรียนรู้วิธีดำเนินการที่คล้ายกันกับความไม่เท่าเทียมกัน ความสามารถในการบวกและคูณความไม่เท่าเทียมกันแบบคำต่อคำมักใช้ในทางปฏิบัติ การกระทำเหล่านี้ช่วยแก้ปัญหาในการประเมินและเปรียบเทียบความหมายของสำนวน

เมื่อตัดสินใจ งานต่างๆบ่อยครั้งที่คุณต้องบวกหรือคูณด้านซ้ายและขวาของอสมการทีละเทอม ในขณะเดียวกันก็มีการกล่าวกันว่าความไม่เท่าเทียมกันนั้นเพิ่มขึ้นหรือทวีคูณ ตัวอย่างเช่น หากนักท่องเที่ยวเดินมากกว่า 20 กม. ในวันแรก และมากกว่า 25 กม. ในวันที่สอง เราสามารถพูดได้ว่าในสองวันเขาเดินมากกว่า 45 กม. ในทำนองเดียวกัน หากความยาวของสี่เหลี่ยมผืนผ้าน้อยกว่า 13 ซม. และความกว้างน้อยกว่า 5 ซม. เราก็บอกได้ว่าพื้นที่ของสี่เหลี่ยมผืนผ้านี้น้อยกว่า 65 ซม. 2

เมื่อพิจารณาตัวอย่างเหล่านี้ มีการใช้สิ่งต่อไปนี้: ทฤษฎีบทการบวกและการคูณอสมการ:

ทฤษฎีบท.เมื่อบวกความไม่เท่าเทียมกันของเครื่องหมายเดียวกัน จะได้ความไม่เท่าเทียมกันของเครื่องหมายเดียวกัน: ถ้า a > b และ c > d แล้ว a + c > b + d

ทฤษฎีบท.เมื่อคูณอสมการของเครื่องหมายเดียวกันซึ่งมีด้านซ้ายและขวาเป็นบวก จะได้ค่าอสมการของเครื่องหมายเดียวกัน: ถ้า a > b, c > d และ a, b, c, d เป็นจำนวนบวก แล้ว ac > bd

อสมการที่มีเครื่องหมาย > (มากกว่า) และ 1/2, 3/4 b, c พร้อมด้วยเครื่องหมายของอสมการเข้มงวด > และในทำนองเดียวกัน อสมการ \(a \geq b \) หมายความว่าจำนวน a คือ มากกว่าหรือเท่ากับ b นั่นคือ . และไม่น้อยกว่า b

อสมการที่มีเครื่องหมาย \(\geq \) หรือเครื่องหมาย \(\leq \) เรียกว่าไม่เข้มงวด ตัวอย่างเช่น \(18 \geq 12 , \; 11 \leq 12 \) ไม่ใช่อสมการที่เข้มงวด

คุณสมบัติทั้งหมดของอสมการเข้มงวดยังใช้ได้กับอสมการที่ไม่เข้มงวดเช่นกัน ยิ่งกว่านั้น หากสำหรับความไม่เท่าเทียมกันที่เข้มงวด เครื่องหมาย > ถือว่าตรงกันข้าม และคุณรู้ว่าในการแก้ปัญหาที่ประยุกต์จำนวนหนึ่ง คุณต้องสร้างแบบจำลองทางคณิตศาสตร์ในรูปแบบของสมการหรือระบบสมการ ต่อไปคุณจะพบว่า แบบจำลองทางคณิตศาสตร์ในการแก้ปัญหาต่างๆ มากมาย มีความไม่เท่าเทียมกันกับสิ่งที่ไม่รู้ เราจะนำเสนอแนวคิดในการแก้ปัญหาความไม่เท่าเทียมกันและวิธีทดสอบว่าตัวเลขที่กำหนดเป็นวิธีแก้ปัญหาของความไม่เท่าเทียมกันโดยเฉพาะหรือไม่

ความไม่เท่าเทียมกันของแบบฟอร์ม
\(ax > b, \quad ax โดยให้ a และ b เป็นตัวเลข ส่วน x เป็นค่าที่ไม่รู้จัก เรียกว่า อสมการเชิงเส้นกับคนหนึ่งที่ไม่รู้จัก.

คำนิยาม.วิธีแก้อสมการโดยมีค่าที่ไม่ทราบคือค่าของค่าที่ไม่ทราบ ซึ่งอสมการนี้จะกลายเป็นอสมการเชิงตัวเลขที่แท้จริง การแก้ไขความไม่เท่าเทียมกันหมายถึงการค้นหาวิธีแก้ปัญหาทั้งหมดหรือพิสูจน์ว่าไม่มีเลย

คุณแก้สมการโดยลดให้เหลือสมการที่ง่ายที่สุด ในทำนองเดียวกัน เมื่อแก้ไขอสมการ เราพยายามลดอสมการเหล่านี้ให้อยู่ในรูปของอสมการธรรมดาโดยใช้คุณสมบัติ

การแก้อสมการระดับสองด้วยตัวแปรตัวเดียว

ความไม่เท่าเทียมกันของแบบฟอร์ม
\(ax^2+bx+c >0 \) และ \(ax^2+bx+c โดยที่ x เป็นตัวแปร a, b และ c เป็นตัวเลขจำนวนหนึ่ง และ \(a \neq 0 \) เรียกว่า อสมการระดับที่สองกับตัวแปรหนึ่งตัว.

การแก้ปัญหาความไม่เท่าเทียมกัน
\(ax^2+bx+c >0 \) หรือ \(ax^2+bx+c ถือได้ว่าเป็นการค้นหาช่วงเวลาที่ฟังก์ชัน \(y= ax^2+bx+c \) รับค่าบวกหรือค่าลบ ค่า ในการทำเช่นนี้ก็เพียงพอที่จะวิเคราะห์ว่ากราฟของฟังก์ชัน \(y= ax^2+bx+c\) อยู่ในระนาบพิกัดอย่างไร: โดยที่กิ่งก้านของพาราโบลาถูกชี้ทิศทาง - ขึ้นหรือลงไม่ว่า พาราโบลาตัดแกน x และถ้ามันตัด แล้วจุดที่ใด

อัลกอริทึมสำหรับแก้อสมการระดับสองด้วยตัวแปรเดียว:
1) ค้นหาการแบ่งแยกของตรีโกณมิติกำลังสอง \(ax^2+bx+c\) และค้นหาว่าตรีโกณมิติมีรากหรือไม่
2) ถ้าตรีโกณมิติมีราก ให้ทำเครื่องหมายไว้บนแกน x และวาดพาราโบลาแผนผังผ่านจุดที่ทำเครื่องหมายไว้ โดยกิ่งก้านของมันจะชี้ขึ้นด้านบนสำหรับ a > 0 หรือด้านล่างสำหรับ 0 หรือด้านล่างสำหรับ 3) หาช่วงเวลาบนแกน x ซึ่งมีจุดพาราโบลาอยู่เหนือแกน x (หากพาราโบลาแก้สมการ \(ax^2+bx+c >0\)) หรือต่ำกว่าแกน x (หากพาราโบลาแก้สมการ ความไม่เท่าเทียมกัน
\(ax^2+bx+c แก้อสมการโดยใช้วิธีช่วงเวลา

พิจารณาฟังก์ชัน
ฉ(x) = (x + 2)(x - 3)(x - 5)

โดเมนของฟังก์ชันนี้คือเซตของตัวเลขทั้งหมด ศูนย์ของฟังก์ชันคือตัวเลข -2, 3, 5 โดยแบ่งโดเมนของคำจำกัดความของฟังก์ชันออกเป็นระยะ \((-\infty; -2), \; (-2; 3), \; ( 3; 5) \) และ \( (5; +\infty)\)

ให้เราดูว่าสัญญาณของฟังก์ชันนี้คืออะไรในแต่ละช่วงเวลาที่ระบุ

นิพจน์ (x + 2)(x - 3)(x - 5) เป็นผลคูณของปัจจัย 3 ตัว เครื่องหมายของแต่ละปัจจัยเหล่านี้ในช่วงเวลาที่พิจารณาแสดงอยู่ในตาราง:

โดยทั่วไป ให้ฟังก์ชันถูกกำหนดโดยสูตร
ฉ(x) = (x-x 1)(x-x 2) ... (x-x n)
โดยที่ x คือตัวแปร และ x 1, x 2, ..., xn คือตัวเลขที่ไม่เท่ากัน ตัวเลข x 1 , x 2 , ..., xn เป็นศูนย์ของฟังก์ชัน ในแต่ละช่วงเวลาที่โดเมนของคำจำกัดความถูกหารด้วยศูนย์ของฟังก์ชัน เครื่องหมายของฟังก์ชันจะยังคงอยู่ และเมื่อผ่านศูนย์ เครื่องหมายก็จะเปลี่ยนไป

คุณสมบัตินี้ใช้เพื่อแก้ความไม่เท่าเทียมกันของแบบฟอร์ม
(x-x 1)(x-x 2) ... (x-x n) > 0,
(x-x 1)(x-x 2) ... (x-x n) โดยที่ x 1, x 2, ..., xn เป็นตัวเลขที่ไม่เท่ากัน

วิธีพิจารณา การแก้อสมการเรียกว่าวิธีแบบเป็นช่วง

ให้เรายกตัวอย่างการแก้ไขอสมการโดยใช้วิธีช่วงเวลา

แก้ปัญหาความไม่เท่าเทียมกัน:

\(x(0.5-x)(x+4) แน่นอนว่า ค่าศูนย์ของฟังก์ชัน f(x) = x(0.5-x)(x+4) คือจุด \(x=0, \; x= \ frac(1)(2) , \; x=-4 \)

เราพล็อตค่าศูนย์ของฟังก์ชันบนแกนตัวเลขและคำนวณเครื่องหมายในแต่ละช่วงเวลา:

เราเลือกช่วงเวลาที่ฟังก์ชันน้อยกว่าหรือเท่ากับศูนย์แล้วจดคำตอบไว้

คำตอบ:
\(x \in \left(-\infty; \; 1 \right) \cup \left[ 4; \; +\infty \right) \)

เซตของจำนวนจริงทั้งหมดสามารถแสดงเป็นชุดของสามชุด ได้แก่ เซตของจำนวนบวก เซตของจำนวนลบ และเซตที่ประกอบด้วยตัวเลขหนึ่งตัว - เลขศูนย์ เพื่อระบุจำนวนนั้น กบวกใช้การบันทึก ก > 0เพื่อระบุจำนวนลบให้ใช้สัญลักษณ์อื่น ก< 0 .

ผลรวมและผลคูณของจำนวนบวกก็เป็นจำนวนบวกเช่นกัน ถ้าเป็นจำนวน กลบแล้วตามด้วยตัวเลข -กเชิงบวก (และในทางกลับกัน) สำหรับจำนวนบวกใดๆ a จะมีจำนวนตรรกยะบวก ร, อะไร ร< а - ข้อเท็จจริงเหล่านี้รองรับทฤษฎีความไม่เท่าเทียมกัน

ตามคำนิยาม ความไม่เท่าเทียมกัน a > b (หรือสิ่งที่เหมือนกันคือ b< a) имеет место в том и только в том случае, если а - b >0 เช่น ถ้าตัวเลข a - b เป็นบวก

โดยเฉพาะการพิจารณาถึงความไม่เท่าเทียมกัน ก< 0 - ความไม่เท่าเทียมกันนี้หมายความว่าอย่างไร? ตามคำจำกัดความข้างต้นก็หมายความว่า 0 - ก > 0, เช่น. -ก > 0หรืออีกนัยหนึ่งคือตัวเลขอะไร -กในเชิงบวก แต่สิ่งนี้จะเกิดขึ้นก็ต่อเมื่อมีจำนวนเท่านั้น กเชิงลบ. ความไม่เท่าเทียมกันดังนั้น ก< 0 หมายความว่าจำนวนนั้น แต่เป็นเชิงลบ

สัญกรณ์ก็มักจะใช้ เกี่ยวกับ(หรือสิ่งที่เหมือนกันคือ บ๊ะ).
บันทึก เกี่ยวกับโดยนิยามแล้วหมายความว่าอย่างใดอย่างหนึ่ง ก > ข, หรือ ก = ข- หากเราพิจารณาบันทึก เกี่ยวกับเป็นคำสั่งไม่แน่นอน จากนั้นเราสามารถเขียนสัญกรณ์ตรรกะทางคณิตศาสตร์ได้

(ก ข) [(ก > ข) วี (ก = ข)]

ตัวอย่างที่ 1อสมการ 5 0, 0 0 จริงหรือไม่?

อสมการ 5 0 เป็นข้อความที่ซับซ้อนซึ่งประกอบด้วยข้อความง่ายๆ สองข้อความที่เชื่อมโยงกันด้วยตรรกะที่เชื่อมโยงกัน “หรือ” (การแยกจากกัน) 5 > 0 หรือ 5 = 0 ข้อความสั่งแรก 5 > 0 เป็นจริง ข้อความสั่งที่สอง 5 = 0 เป็นเท็จ ตามคำจำกัดความของการแยกส่วน ข้อความที่ซับซ้อนเช่นนี้จะเป็นจริง

รายการ 00 ถูกกล่าวถึงในทำนองเดียวกัน

ความไม่เท่าเทียมกันของแบบฟอร์ม ก > ข, ก< b เราจะเรียกพวกเขาว่าเข้มงวดและไม่เท่าเทียมกันในรูปแบบ ab,ab- ไม่เข้มงวด

อสมการ ก > ขและ ค > ง(หรือ ก< b และ กับ< d ) จะเรียกว่าอสมการที่มีความหมายเหมือนกันและอสมการ ก > ขและ ค< d - ความไม่เท่าเทียมกันของความหมายตรงกันข้าม โปรดทราบว่าคำทั้งสองนี้ (ความไม่เท่าเทียมกันที่มีความหมายเหมือนกันและตรงกันข้าม) อ้างอิงถึงรูปแบบการเขียนความไม่เท่าเทียมกันเท่านั้น และไม่ใช่ข้อเท็จจริงที่แสดงออกโดยความไม่เท่าเทียมกันเหล่านี้ ดังนั้นในเรื่องของความไม่เท่าเทียมกัน ก< b ความไม่เท่าเทียมกัน กับ< d คือความไม่เท่าเทียมกันซึ่งมีความหมายเดียวกันและอยู่ในสัญกรณ์ ง>ค(หมายถึงสิ่งเดียวกัน) - ความไม่เท่าเทียมกันของความหมายตรงกันข้าม

ประกอบกับความไม่เท่าเทียมกันของฟอร์ม ก>ข, เกี่ยวกับมีการใช้สิ่งที่เรียกว่าความไม่เท่าเทียมกันสองเท่านั่นคือความไม่เท่าเทียมกันของรูปแบบ ก< с < b , เครื่องปรับอากาศ< b , ก< cb ,
กซีบี- ตามคำนิยาม เป็นบันทึก

ก< с < b (1)
หมายความว่าความไม่เท่าเทียมกันทั้งสองถือ:

ก< с และ กับ< b.

ความไม่เท่าเทียมกันมีความหมายคล้ายกัน เอซีบี เอซี< b, а < сb.

อสมการสองเท่า (1) สามารถเขียนได้ดังนี้:

(ก< c < b) [(a < c) & (c < b)]

และความไม่เท่าเทียมกันสองเท่า ก ≤ ค ≤ ขสามารถเขียนได้ในรูปแบบดังนี้

(ก ค ข) [(ก< c)V(a = c) & (c < b)V(c = b)]

ให้เราดำเนินการนำเสนอคุณสมบัติพื้นฐานและกฎการดำเนินการเกี่ยวกับความไม่เท่าเทียมกันโดยตกลงกันว่าในบทความนี้ตัวอักษร ก ข คแทนจำนวนจริง และ nหมายถึงจำนวนธรรมชาติ

1) ถ้า a > b และ b > c แล้ว a > c (การถ่ายทอด)

การพิสูจน์.

เนื่องจากตามเงื่อนไข ก > ขและ ข > คแล้วตัวเลข ก - ขและ ข - คเป็นบวก และด้วยเหตุนี้จึงเป็นจำนวน ก - ค = (ก - ข) + (ข - ค)เนื่องจากผลรวมของจำนวนบวกก็เป็นบวกเช่นกัน ความหมายตามคำนิยามก็คือว่า ก > ค.

2) ถ้า a > b ดังนั้นสำหรับ c ใดๆ จะมีอสมการ a + c > b + c อยู่

การพิสูจน์.

เพราะ ก > ขแล้วตามด้วยหมายเลข ก - ขในเชิงบวก ดังนั้นจำนวน (a + c) - (b + c) = a + c - b - c = a - bเป็นบวกเช่นกัน เช่น
ก + ค > ข + ค

3) ถ้า a + b > c ดังนั้น a > b - cนั่นคือคำใด ๆ ที่สามารถถ่ายโอนจากส่วนหนึ่งของความไม่เท่าเทียมกันไปยังอีกส่วนหนึ่งได้โดยการเปลี่ยนเครื่องหมายของคำนี้ไปในทางตรงกันข้าม

หลักฐานตามมาจากคุณสมบัติ 2) ก็เพียงพอแล้วสำหรับความไม่เท่าเทียมกันทั้งสองฝ่าย ก + ข > คเพิ่มหมายเลข -ข.

4) ถ้า a > b และ c > d แล้ว a + c > b + dนั่นคือเมื่อบวกความไม่เท่าเทียมกันสองรายการที่มีความหมายเดียวกันก็จะได้ความไม่เท่าเทียมกันในความหมายเดียวกัน

การพิสูจน์.

โดยอาศัยคำนิยามของความไม่เท่าเทียมกันก็เพียงพอที่จะแสดงให้เห็นความแตกต่าง
(ก + ค) - (ข + ค)เชิงบวก. ความแตกต่างนี้สามารถเขียนได้ดังนี้:
(ก + ค) - (ข + ง) = (ก - ข) + (ค - ง).
เนื่องจากตามเงื่อนไขของจำนวน ก - ขและ ซีดีเป็นบวกแล้ว (ก + ค) - (ข + ง)มีจำนวนบวกด้วย

ผลที่ตามมา จากกฎข้อ 2) และ 4) เป็นไปตามนั้น กฎถัดไปการลบอสมการ: ถ้า ก > ข, ค > ง, ที่ ก - ง > ข - ค(เพื่อพิสูจน์ ก็เพียงพอที่จะใช้อสมการทั้งสองด้าน ก + ค > ข + งเพิ่มหมายเลข - ซีดี).

5) ถ้า a > b แล้วสำหรับ c > 0 เรามี ac > bc และสำหรับ c< 0 имеем ас < bc.

กล่าวอีกนัยหนึ่ง เมื่อคูณทั้งสองด้านของอสมการด้วยจำนวนบวก เครื่องหมายอสมการจะยังคงอยู่ (เช่น ได้รับความไม่เท่าเทียมกันซึ่งมีความหมายเดียวกัน) แต่เมื่อคูณด้วยจำนวนลบ เครื่องหมายอสมการจะเปลี่ยนเป็นค่าตรงกันข้าม (นั่นคือได้รับความไม่เท่าเทียมกันของความหมายตรงกันข้าม

การพิสูจน์.

ถ้า ก > ข, ที่ ก - ขเป็นจำนวนบวก ดังนั้นสัญญาณของความแตกต่าง เอซี-บีซี = แท็กซี่)ตรงกับเครื่องหมายของตัวเลข กับ: ถ้า กับเป็นจำนวนบวก แล้วก็ผลต่าง เอซี - บีซีเป็นบวก ดังนั้น เอซี > พ.ศ, และถ้า กับ< 0 แล้วความแตกต่างนี้จึงเป็นลบ ดังนั้น บีซี - เอซีเชิงบวก เช่น พ.ศ. > ไฟฟ้ากระแสสลับ.

6) ถ้า a > b > 0 และ c > d > 0 แล้ว ac > bdนั่นคือ ถ้าเงื่อนไขทั้งหมดของอสมการทั้งสองที่มีความหมายเดียวกันเป็นบวก เมื่อคูณอสมการเหล่านี้ทีละเทอม ก็จะได้อสมการที่มีความหมายเดียวกัน

การพิสูจน์.

เรามี ไฟฟ้ากระแสสลับ - bd = ไฟฟ้ากระแสสลับ - bc + bc - bd = ค(ก - ข) + ข(ค - ง)- เพราะ ค > 0, ข > 0, a - b > 0, c - d > 0 จากนั้น ac - bd > 0 เช่น ac > bd

ความคิดเห็นจากการพิสูจน์ก็ชัดเจนว่าสภาพ ง > 0ในการกำหนดคุณสมบัติ 6) ไม่สำคัญ: เพื่อให้คุณสมบัตินี้ถูกต้องก็เพียงพอแล้วที่จะตรงตามเงื่อนไข ก > ข > 0, ค > ง, ค > 0- ถ้า (หากความไม่เท่าเทียมกันสำเร็จแล้ว ก > ข, ค > ง) ตัวเลข ก ข คจะไม่เป็นบวกทั้งหมดแล้วความไม่เท่าเทียมกัน เครื่องปรับอากาศ > bdไม่อาจเติมเต็มได้ เช่น เมื่อใด ก = 2, ข =1, ค= -2, ง= -3 เรามี ก > ข, ค > งแต่ความไม่เท่าเทียมกัน เครื่องปรับอากาศ > bd(เช่น -4 > -3) ล้มเหลว ดังนั้น ข้อกำหนดที่ว่าตัวเลข a, b, c ต้องเป็นค่าบวกในการกำหนดคุณสมบัติ 6) จึงเป็นสิ่งสำคัญ

7) ถ้า a ≥ b > 0 และ c > d > 0 แล้ว (การหารอสมการ)

การพิสูจน์.

เรามี ตัวเศษของเศษส่วนทางขวาเป็นค่าบวก (ดูคุณสมบัติ 5), 6)) ส่วนตัวส่วนก็เป็นบวกเช่นกัน เพราะฉะนั้น,. นี่เป็นการพิสูจน์คุณสมบัติ 7)

ความคิดเห็นเรามาสังเกตสิ่งสำคัญกัน กรณีพิเศษกฎข้อ 7) จะได้เมื่อ a = b = 1: ถ้า c > d > 0 แล้ว ดังนั้นหากเงื่อนไขของความไม่เท่าเทียมกันเป็นบวก เมื่อส่งผ่านไปยังส่วนกลับ เราจะได้ความไม่เท่าเทียมกันในความหมายตรงกันข้าม เราขอเชิญชวนผู้อ่านให้ตรวจสอบว่ากฎนี้มีอยู่ใน 7) ถ้า ab > 0 และ c > d > 0 ดังนั้น (การหารอสมการ)

การพิสูจน์. ที่.

เราได้พิสูจน์คุณสมบัติหลายประการของอสมการที่เขียนโดยใช้เครื่องหมายข้างต้นแล้ว > (มากกว่า). อย่างไรก็ตาม คุณสมบัติทั้งหมดนี้สามารถกำหนดได้โดยใช้เครื่องหมาย < (น้อยกว่า) เนื่องจากความไม่เท่าเทียมกัน ข< а ความหมายตามคำจำกัดความเช่นเดียวกับความไม่เท่าเทียมกัน ก > ข- นอกจากนี้ ดังที่ง่ายต่อการตรวจสอบ คุณสมบัติที่พิสูจน์แล้วข้างต้นจะถูกเก็บรักษาไว้สำหรับความไม่เท่าเทียมกันที่ไม่เข้มงวด ตัวอย่างเช่น คุณสมบัติ 1) สำหรับอสมการไม่เข้มงวดจะมีรูปแบบดังนี้: if ab และ bc, ที่ เครื่องปรับอากาศ.

แน่นอนว่าสิ่งที่กล่าวมาข้างต้นไม่ได้จำกัดคุณสมบัติทั่วไปของอสมการ นอกจากนี้ยังมี ทั้งบรรทัดความไม่เท่าเทียมกัน ปริทัศน์ที่เกี่ยวข้องกับการพิจารณากำลัง เลขชี้กำลัง ลอการิทึม และ ฟังก์ชันตรีโกณมิติ- แนวทางทั่วไปในการเขียนอสมการประเภทนี้มีดังนี้ หากฟังก์ชั่นบางอย่าง ย = ฉ(x)เพิ่มขึ้นอย่างซ้ำซากจำเจในส่วนนี้ [ก ข]จากนั้นสำหรับ x 1 > x 2 (โดยที่ x 1 และ x 2 อยู่ในส่วนนี้) เรามี f (x 1) > ฉ(x 2). ในทำนองเดียวกันหากฟังก์ชั่น ย = ฉ(x)ลดลงอย่างน่าเบื่อตามช่วงเวลา [ก ข], แล้วเมื่อไหร่ x 1 > x 2 (ที่ไหน x1และ เอ็กซ์ 2 อยู่ในส่วนนี้) เรามี ฉ(x 1)< f(x 2 - แน่นอนว่าสิ่งที่กล่าวมานั้นไม่ต่างจากคำจำกัดความของความซ้ำซากจำเจ แต่เทคนิคนี้สะดวกมากในการท่องจำและเขียนความไม่เท่าเทียมกัน

ตัวอย่างเช่น สำหรับจำนวนธรรมชาติใดๆ ของฟังก์ชัน y = xnกำลังเพิ่มขึ้นอย่างซ้ำซากจำเจไปตามรังสี }