เนื่องจากมีเพียงไม่กี่คนที่มีความคิดทางคณิตศาสตร์ ฉันจะพูดถึงการค้นพบทางวิทยาศาสตร์ที่ใหญ่ที่สุด - การพิสูจน์เบื้องต้นของทฤษฎีบทสุดท้ายของแฟร์มาต์ - ในภาษาโรงเรียนที่เข้าใจได้มากที่สุด

พบข้อพิสูจน์สำหรับกรณีพิเศษ (สำหรับระดับอย่างง่าย n>2) ซึ่ง (และสำหรับกรณี n=4) ทุกกรณีที่มีจำนวนประกอบ n สามารถลดลงได้อย่างง่ายดาย

ดังนั้น เราต้องพิสูจน์ว่าสมการ A^n=C^n-B^n ไม่มีคำตอบเป็นจำนวนเต็ม (เครื่องหมาย ^ ในที่นี้หมายถึงระดับ)

การพิสูจน์จะดำเนินการในระบบจำนวนที่มีฐานอย่างง่าย n ในกรณีนี้ ตัวเลขสุดท้ายในแต่ละตารางสูตรคูณจะไม่ซ้ำกัน ในระบบทศนิยมปกติ สถานการณ์จะแตกต่างออกไป ตัวอย่างเช่น เมื่อคูณตัวเลข 2 ด้วยทั้ง 1 และ 6 ผลิตภัณฑ์ทั้งสอง - 2 และ 12 - จะลงท้ายด้วยตัวเลขเดียวกัน (2) และตัวอย่างเช่น ในระบบเซพเทนารีของเลข 2 ตัวเลขสุดท้ายทั้งหมดจะต่างกัน: 0x2=...0, 1x2=...2, 2x2=...4, 3x2=...6, 4x2 =...1, 5x2=...3, 6x2=...5 โดยมีชุดเลขท้าย 0, 2, 4, 6, 1, 3, 5

ด้วยคุณสมบัตินี้ สำหรับตัวเลข A ใดๆ ที่ไม่ได้ลงท้ายด้วยศูนย์ (และในความเท่าเทียมกันของแฟร์มาต์ หลักสุดท้ายของตัวเลข A หรือ B หลังจากหารความเท่าเทียมกันด้วยตัวหารร่วมของตัวเลข A, B, C จะไม่ใช่ เท่ากับศูนย์) คุณสามารถเลือกปัจจัย g ได้ โดยที่ตัวเลข Ag จะมีจุดสิ้นสุดที่ยาวตามต้องการของแบบฟอร์ม 000...001 ด้วยจำนวน g นี้เองที่เราคูณเลขฐาน A, B, C ทั้งหมดในความเท่าเทียมกันของแฟร์มาต์ ในกรณีนี้เราจะทำให้หน่วยลงท้ายค่อนข้างยาว คือ ยาวกว่าเลข (k) ของศูนย์ที่อยู่ท้ายเลข U=A+B-C สองหลัก

ตัวเลข U ไม่เท่ากับศูนย์ - มิฉะนั้น C=A+B และ A^n<(А+В)^n-B^n, т.е. равенство Ферма является неравенством.

อันที่จริงนี่คือการเตรียมความเท่าเทียมกันของแฟร์มาต์ทั้งหมดสำหรับการศึกษาโดยสรุปและขั้นสุดท้าย สิ่งเดียวที่เราจะทำคือเขียนทางด้านขวามือของความเท่าเทียมกันของแฟร์มาต์ – C^n-B^n โดยใช้สูตรการสลายตัวแบบโรงเรียน: C^n-B^n=(C-B)P หรือ aP และเนื่องจากต่อไปเราจะดำเนินการ (คูณและเพิ่ม) ด้วยตัวเลขของ (k+2) - ตอนจบหลักของตัวเลข A, B, C เท่านั้น จากนั้นเราไม่สามารถนำส่วนที่นำของพวกเขามาพิจารณาและทิ้งพวกมันไป (ปล่อยให้ ข้อเท็จจริงเพียงข้อเดียวในความทรงจำ: ทางด้านซ้ายของความเสมอภาคของแฟร์มาต์คือพลัง)

สิ่งเดียวที่ควรกล่าวถึงคือตัวเลขหลักสุดท้ายของตัวเลข a และ P ในความเท่าเทียมกันดั้งเดิมของแฟร์มาต์ ตัวเลข P จะลงท้ายด้วยเลข 1 ซึ่งตามมาจากสูตรทฤษฎีบทเล็กๆ ของแฟร์มาต์ ซึ่งพบได้ในหนังสืออ้างอิง และหลังจากการคูณความเท่าเทียมกันของแฟร์มาต์ด้วยจำนวน g^n แล้ว จำนวน P จะถูกคูณด้วยจำนวน g ยกกำลัง n-1 ซึ่งตามทฤษฎีบทเล็กๆ ของแฟร์มาต์ ก็ลงท้ายด้วยเลข 1 เช่นกัน ดังนั้นในความเท่าเทียมกันของแฟร์มาต์ที่เทียบเท่าใหม่ เลข P ลงท้ายด้วย 1 และถ้า A ลงท้ายด้วย 1 แล้ว A^n ก็ลงท้ายด้วย 1 ด้วย ดังนั้น ตัวเลข a จึงลงท้ายด้วย 1 ด้วย

ดังนั้นเราจึงมีสถานการณ์เริ่มต้น: ตัวเลขสุดท้าย A, a, P ของตัวเลข A, a, P ลงท้ายด้วยเลข 1

จากนั้น การดำเนินการที่น่ารักและน่าหลงใหลก็เริ่มต้นขึ้น โดยเรียกตามความชอบว่า "โรงสี" โดยการนำตัวเลขที่ตามมาคือ a"", a""" และอื่นๆ ตัวเลข a เราคำนวณได้อย่าง "ง่ายดาย" อย่างยิ่งว่าพวกมันทั้งหมด เท่ากับศูนย์ด้วย Word ฉันใส่คำว่า "ง่าย" ในเครื่องหมายคำพูดเพราะมนุษยชาติไม่สามารถหากุญแจสู่ "ง่าย" นี้เป็นเวลา 350 ปี! ^(k+2) มันไม่คุ้มที่จะให้ความสนใจกับเทอมที่สองของผลรวมนี้ - ในการพิสูจน์เพิ่มเติมเราได้ละทิ้งตัวเลขทั้งหมดหลัง (k+2)th ของตัวเลข (และทำให้การวิเคราะห์ง่ายขึ้นอย่างมาก) ดังนั้น หลังจากละทิ้งหมายเลขส่วนหัวแล้ว ความเท่าเทียมกันของ Fermat จะอยู่ในรูปแบบ: ...1 =aq^(n-1) โดยที่ a และ q ไม่ใช่ตัวเลข แต่เป็นเพียงจุดสิ้นสุดของตัวเลข a และ q! (ฉันไม่แนะนำสัญลักษณ์ใหม่เนื่องจากจะทำให้อ่านยาก)

คำถามเชิงปรัชญาสุดท้ายยังคงอยู่: เหตุใดจึงสามารถแสดงตัวเลข P เป็น P=q^(n-1)+Qn^(k+2) ได้ คำตอบนั้นง่ายมาก เนื่องจากจำนวนเต็ม P ที่มี 1 ต่อท้ายสามารถแสดงในรูปแบบนี้ได้ และมีลักษณะเฉพาะตัว (สามารถแสดงได้หลายวิธี แต่เราไม่ต้องการสิ่งนั้น) อันที่จริง สำหรับ P=1 คำตอบนั้นชัดเจน: P=1^(n-1) สำหรับ Р=hn+1 คือตัวเลข q=(n-h)n+1 ซึ่งตรวจสอบได้ง่ายด้วยการแก้สมการ [(n-h)n+1]^(n-1)==hn+1 โดยใช้ตัวเลขสองหลัก ตอนจบ และอื่นๆ (แต่เราไม่ต้องการการคำนวณเพิ่มเติม เนื่องจากเราเพียงแต่ต้องแสดงตัวเลขในรูปแบบ P=1+Qn^t)

วุ้ย ปรัชญาจบลงแล้ว คุณสามารถไปสู่การคำนวณในระดับชั้นประถมศึกษาปีที่ 2 ได้ บางทีอาจแค่จำสูตรทวินามของนิวตันอีกครั้ง

ดังนั้น เรามาแนะนำตัวเลข a"" (ในตัวเลข a=a""n+1) และใช้มันเพื่อคำนวณตัวเลข q"" (ในตัวเลข q=q""n+1):
...01=(a""n+1)(q""n+1)^(n-1) หรือ...01=(a""n+1)[(n-q"")n+ 1 ] จากไหน q""=a""

และตอนนี้ทางด้านขวาของความเสมอภาคของแฟร์มาต์สามารถเขียนใหม่ได้เป็น:
A^n=(a""n+1)^n+Dn^(k+2) โดยที่เราไม่ได้สนใจค่าของตัวเลข D

ตอนนี้เรามาถึงข้อสรุปที่เด็ดขาด ตัวเลข a""n+1 คือการลงท้ายด้วยตัวเลขสองหลักของตัวเลข A ดังนั้น ตามบทแทรกง่ายๆ UNIQUELY จึงกำหนดตัวเลขหลักที่สามของระดับ A^n และยิ่งไปกว่านั้นจากการขยายตัวของทวินามของนิวตัน
(a""n+1)^n โดยคำนึงว่าแต่ละเทอมของการขยาย (ยกเว้นเทอมแรกซึ่งไม่สามารถเปลี่ยนสภาพอากาศได้!) จะมีการเพิ่มปัจจัยอย่างง่าย n (ฐานตัวเลข!) เข้าไปด้วย จึงชัดเจน ว่าหลักที่สามนี้เท่ากับ a"" แต่ด้วยการคูณความเท่าเทียมกันของแฟร์มาต์ด้วย g^n เราจะเปลี่ยน k+1 หลักก่อนเลข 1 ตัวสุดท้ายในเลข A ให้เป็น 0 ดังนั้น a""=0!!!

ดังนั้นเราจึงเสร็จสิ้นวงจร: เมื่อป้อน a"" เราก็พบว่า q""=a"" และสุดท้ายคือ a""=0!

ยังคงต้องบอกว่าหลังจากทำการคำนวณที่คล้ายกันโดยสิ้นเชิงและตัวเลข k หลักถัดไป เราจะได้ความเท่าเทียมกันสุดท้าย: (k + 2) - หลักที่ลงท้ายด้วยตัวเลข a หรือ C-B เช่นเดียวกับตัวเลข A นั้นเท่ากัน เป็น 1 แต่แล้วหลักที่ (k+2) ของตัวเลข C-A-B เท่ากับศูนย์ ในขณะที่มันไม่เท่ากับศูนย์!!!

อันที่จริงมันคือข้อพิสูจน์ทั้งหมด เพื่อให้เข้าใจสิ่งนี้ ไม่จำเป็นเลยที่จะต้องมีการศึกษาระดับสูง และโดยเฉพาะอย่างยิ่ง การเป็นนักคณิตศาสตร์มืออาชีพ อย่างไรก็ตาม ผู้เชี่ยวชาญยังคงนิ่งเงียบ...

ข้อความที่สามารถอ่านได้ของหลักฐานฉบับเต็มอยู่ที่นี่:

รีวิว

สวัสดีวิคเตอร์ ฉันชอบเรซูเม่ของคุณ “อย่าปล่อยให้ตายก่อนตาย” ฟังดูดีแน่นอน พูดตามตรง ฉันรู้สึกทึ่งกับการเผชิญหน้ากับทฤษฎีบทของแฟร์มาต์ในร้อยแก้ว! เธออยู่ที่นี่เหรอ? มีสถานที่ทางวิทยาศาสตร์ วิทยาศาสตร์ยอดนิยม และกาน้ำชา มิฉะนั้นขอขอบคุณสำหรับงานวรรณกรรมของคุณ
ขอแสดงความนับถืออันย่า

เรียนคุณย่า แม้จะมีการเซ็นเซอร์ค่อนข้างเข้มงวด แต่ Prose ก็อนุญาตให้คุณเขียนเกี่ยวกับทุกสิ่งได้ สถานการณ์ของทฤษฎีบทของแฟร์มาต์เป็นดังนี้: ฟอรัมทางคณิตศาสตร์ขนาดใหญ่ปฏิบัติต่อความสงสัยของ Fermatists ด้วยความหยาบคาย และโดยทั่วไปแล้วปฏิบัติต่อพวกเขาอย่างดีที่สุดเท่าที่จะทำได้ อย่างไรก็ตาม ฉันนำเสนอข้อพิสูจน์เวอร์ชันล่าสุดในฟอรั่มรัสเซีย อังกฤษ และฝรั่งเศสขนาดเล็ก ยังไม่มีใครเสนอข้อโต้แย้งใด ๆ และฉันแน่ใจว่าจะไม่มีใครเสนอข้อโต้แย้งใด ๆ (หลักฐานได้รับการตรวจสอบอย่างรอบคอบ) ในวันเสาร์ ฉันจะเผยแพร่บันทึกเชิงปรัชญาเกี่ยวกับทฤษฎีบท
แทบไม่มีคนร้อยแก้วเลย และถ้าคุณไม่ไปเที่ยวกับพวกเขา ในไม่ช้าพวกเขาก็จะหายไป
ผลงานของฉันเกือบทั้งหมดนำเสนอใน Prose ดังนั้นฉันจึงรวมหลักฐานไว้ที่นี่ด้วย
แล้วพบกันใหม่

คนอิจฉาอ้างว่านักคณิตศาสตร์ชาวฝรั่งเศส ปิแอร์ แฟร์มาต์ เขียนชื่อของเขาในประวัติศาสตร์ด้วยวลีเพียงวลีเดียว ตรงขอบของต้นฉบับซึ่งมีการกำหนดทฤษฎีบทอันโด่งดังในปี 1637 เขาได้เขียนข้อความว่า “ฉันพบวิธีแก้ปัญหาที่น่าทึ่งแล้ว แต่ไม่มีที่ว่างเพียงพอที่จะใส่ไว้ที่นี่” จากนั้นการแข่งขันทางคณิตศาสตร์ที่น่าทึ่งก็เริ่มขึ้น โดยมีนักวิทยาศาสตร์ผู้โดดเด่น กองทัพมือสมัครเล่นก็เข้าร่วมด้วย

อะไรคือความร้ายกาจของปัญหาของแฟร์มาต์? เมื่อมองแวบแรกแม้แต่เด็กนักเรียนก็สามารถเข้าใจได้

ขึ้นอยู่กับทฤษฎีบทพีทาโกรัสที่ทุกคนรู้จัก: ในรูปสามเหลี่ยมมุมฉาก กำลังสองของด้านตรงข้ามมุมฉากจะเท่ากับผลรวมของกำลังสองของขา: x 2 + y 2 = z 2 แฟร์มาต์แย้งว่า: สมการสำหรับกำลังใดๆ ที่มากกว่าสองไม่มีคำตอบเป็นจำนวนเต็ม

มันจะดูเหมือนง่าย ออกไปและนี่คือคำตอบ ไม่น่าแปลกใจที่สถาบันการศึกษาในประเทศต่างๆ สถาบันวิทยาศาสตร์ แม้แต่กองบรรณาธิการหนังสือพิมพ์ ก็เต็มไปด้วยหลักฐานนับหมื่น จำนวนของพวกเขานั้นไม่เคยมีมาก่อน เป็นรองจากโครงการ "การเคลื่อนไหวตลอดกาล" เท่านั้น แต่หากวิทยาศาสตร์ที่จริงจังไม่ได้พิจารณาแนวคิดบ้า ๆ เหล่านี้มาเป็นเวลานานแล้วงานของ "เกษตรกร" ก็จะได้รับการศึกษาอย่างซื่อสัตย์และมีความสนใจ และอนิจจามันพบข้อผิดพลาด พวกเขากล่าวว่ากว่าสามศตวรรษที่สุสานทางคณิตศาสตร์ทั้งหมดของการแก้ทฤษฎีบทได้ก่อตัวขึ้น

พวกเขาพูดไม่ใช่เพื่ออะไร: ข้อศอกอยู่ใกล้ แต่คุณจะไม่กัด หลายปี ทศวรรษ ศตวรรษผ่านไป งานของแฟร์มาต์ดูน่าประหลาดใจและน่าดึงดูดใจมากขึ้นเรื่อยๆ ดูเหมือนง่าย แต่กลับกลายเป็นว่ายากเกินไปสำหรับการพัฒนาของกล้ามเนื้อที่เติบโตอย่างรวดเร็ว มนุษย์ได้แยกอะตอมออกไปแล้ว ไปถึงยีน และได้เหยียบดวงจันทร์ แต่แฟร์มาต์กลับไม่ยอมแพ้ ยังคงล่อลวงลูกหลานของเขาด้วยความหวังที่ผิดๆ ต่อไป

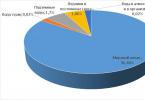
อย่างไรก็ตาม ความพยายามที่จะเอาชนะจุดสูงสุดทางวิทยาศาสตร์ไม่ได้ไร้ประโยชน์ ออยเลอร์ผู้ยิ่งใหญ่ก้าวแรกโดยการพิสูจน์ทฤษฎีบทในระดับที่สี่ จากนั้นจึงพิสูจน์ทฤษฎีบทในระดับที่สาม ในตอนท้ายของศตวรรษที่ 19 เอิร์นส์ คุมเมอร์ ชาวเยอรมัน เพิ่มจำนวนองศาเป็นหนึ่งร้อย ในที่สุดนักวิทยาศาสตร์ก็เพิ่มจำนวนนี้เป็น 100,000 ด้วยคอมพิวเตอร์ แต่แฟร์มาต์กำลังพูดถึงระดับใดก็ได้ นั่นคือประเด็นทั้งหมด

แน่นอน นักวิทยาศาสตร์ไม่ได้ทนทุกข์ทรมานกับปัญหานี้เพราะความสนใจด้านกีฬา David Hilbert นักคณิตศาสตร์ชื่อดังกล่าวว่าทฤษฎีบทนี้เป็นตัวอย่างว่าปัญหาที่ดูเหมือนไม่มีนัยสำคัญสามารถส่งผลกระทบอย่างใหญ่หลวงต่อวิทยาศาสตร์ได้อย่างไร นักวิทยาศาสตร์ได้เปิดโลกทัศน์ทางคณิตศาสตร์ใหม่อย่างสมบูรณ์ ตัวอย่างเช่น วางรากฐานของทฤษฎีจำนวน พีชคณิต และทฤษฎีฟังก์ชัน

แต่ทฤษฎีบทอันยิ่งใหญ่ก็ถูกยึดครองในปี 1995 Andrew Wiles ชาวอเมริกันจากมหาวิทยาลัยพรินซ์ตันนำเสนอวิธีแก้ปัญหาของเธอ และได้รับการยอมรับอย่างเป็นทางการจากชุมชนวิทยาศาสตร์ เขาสละเวลากว่าเจ็ดปีในชีวิตเพื่อค้นหาหลักฐาน ตามที่นักวิทยาศาสตร์กล่าวไว้ งานที่โดดเด่นนี้ได้รวบรวมผลงานของนักคณิตศาสตร์หลายคนเข้าด้วยกัน โดยฟื้นฟูความเชื่อมโยงที่ขาดหายไประหว่างส่วนต่างๆ ของงาน

ดังนั้น การประชุมสุดยอดจึงได้เกิดขึ้นแล้ว และวิทยาศาสตร์ก็ได้รับคำตอบแล้ว” ยูริ วิชเนียคอฟ เลขาธิการวิทยาศาสตร์ของภาควิชาคณิตศาสตร์ของ Russian Academy of Sciences ซึ่งเป็นแพทย์ศาสตร์ดุษฎีบัณฑิต กล่าวกับผู้สื่อข่าวของ RG - ทฤษฎีบทนี้ได้รับการพิสูจน์แล้ว แม้ว่าจะไม่ใช่วิธีที่ง่ายที่สุดก็ตาม ดังที่แฟร์มาต์ยืนยันเอง และตอนนี้ผู้ที่ต้องการสามารถพิมพ์เวอร์ชันของตนเองได้

อย่างไรก็ตาม ครอบครัวของ “ชาวนา” จะไม่ยอมรับหลักฐานของไวล์สเลย ไม่ พวกเขาไม่ได้ปฏิเสธการตัดสินใจของชาวอเมริกัน เพราะมันซับซ้อนมากและดังนั้นจึงเข้าใจได้เฉพาะกับผู้เชี่ยวชาญในวงแคบเท่านั้น แต่ไม่ใช่หนึ่งสัปดาห์ผ่านไปโดยไม่มีการเปิดเผยใหม่จากผู้สนใจรายอื่นที่ปรากฏบนอินเทอร์เน็ต "ในที่สุดก็ยุติมหากาพย์ระยะยาว"

อย่างไรก็ตามเมื่อวานนี้ Vsevolod Yarosh หนึ่งใน "นักปุ๋ย" ที่เก่าแก่ที่สุดในประเทศของเราเรียกว่ากองบรรณาธิการของ "RG": "และคุณรู้ว่าฉันพิสูจน์ทฤษฎีบทของแฟร์มาต์ต่อหน้า Wiles ยิ่งกว่านั้นฉันพบข้อผิดพลาดใน ซึ่งฉันเขียนถึงอาร์โนลด์นักวิชาการคณิตศาสตร์ที่โดดเด่นของเราโดยขอให้ตีพิมพ์เกี่ยวกับเรื่องนี้ในวารสารวิทยาศาสตร์ ตอนนี้ฉันกำลังรอคำตอบ ฉันก็สอดคล้องกับ French Academy of Sciences เกี่ยวกับเรื่องนี้ด้วย”

และตอนนี้ตามที่รายงานในสื่อหลายแห่ง ผู้ที่ชื่นชอบอีกคนหนึ่ง อดีตนักออกแบบทั่วไปของซอฟต์แวร์ Polyot จาก Omsk แพทย์สาขาวิทยาศาสตร์เทคนิค Alexander Ilyin ด้วย "ความสง่างามเล็กน้อย" เปิดเผยความลับอันยิ่งใหญ่ของคณิตศาสตร์ วิธีแก้ปัญหากลายเป็นเรื่องง่ายและสั้นมากจนพอดีกับส่วนเล็กๆ ของพื้นที่หนังสือพิมพ์ของสิ่งพิมพ์กลางฉบับหนึ่ง

บรรณาธิการของ RG หันไปหาสถาบันคณิตศาสตร์ชั้นนำของประเทศที่ตั้งชื่อตาม Steklov RAS พร้อมคำร้องขอประเมินการตัดสินใจครั้งนี้ นักวิทยาศาสตร์มีความชัดเจน: ไม่มีใครแสดงความคิดเห็นในสิ่งพิมพ์ของหนังสือพิมพ์ได้ แต่หลังจากการโน้มน้าวใจอย่างมากและคำนึงถึงความสนใจที่เพิ่มขึ้นในปัญหาที่มีชื่อเสียงพวกเขาก็ตกลงกัน ตามที่กล่าวไว้ มีข้อผิดพลาดพื้นฐานหลายประการเกิดขึ้นในการพิสูจน์ล่าสุดที่เผยแพร่ อย่างไรก็ตาม แม้แต่นักศึกษาคณะคณิตศาสตร์ก็สามารถสังเกตเห็นพวกเขาได้อย่างง่ายดาย

ถึงกระนั้น บรรณาธิการก็ต้องการได้รับข้อมูลโดยตรง ยิ่งกว่านั้นเมื่อวานนี้ที่ Academy of Aviation and Aeronautics Ilyin ควรจะนำเสนอหลักฐานของเขา อย่างไรก็ตาม ปรากฏว่ามีเพียงไม่กี่คนที่รู้เกี่ยวกับสถาบันดังกล่าว แม้แต่ในหมู่ผู้เชี่ยวชาญก็ตาม และเมื่อเราค้นหาหมายเลขโทรศัพท์ของเลขาธิการวิทยาศาสตร์ขององค์กรนี้ด้วยความยากลำบากที่สุด ปรากฎว่าเขาไม่สงสัยด้วยซ้ำว่าเหตุการณ์ประวัติศาสตร์ดังกล่าวกำลังจะเกิดขึ้นที่นั่น กล่าวโดยสรุป ผู้สื่อข่าว RG ล้มเหลวในการเป็นสักขีพยานในความรู้สึกของโลก

1

Ivliev Yu.A.

บทความนี้มีเนื้อหาเกี่ยวกับคำอธิบายข้อผิดพลาดทางคณิตศาสตร์พื้นฐานที่เกิดขึ้นในกระบวนการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์เมื่อปลายศตวรรษที่ 20 ข้อผิดพลาดที่ค้นพบไม่เพียงแต่บิดเบือนความหมายที่แท้จริงของทฤษฎีบทเท่านั้น แต่ยังขัดขวางการพัฒนาแนวทางสัจพจน์ใหม่ในการศึกษาพลังของตัวเลขและอนุกรมของตัวเลขตามธรรมชาติอีกด้วย

ในปี 1995 มีการตีพิมพ์บทความซึ่งมีขนาดใกล้เคียงกับหนังสือ และรายงานการพิสูจน์ทฤษฎีบทอันยิ่งใหญ่ (สุดท้าย) ของแฟร์มาต์ (WTF) ที่มีชื่อเสียง (สำหรับประวัติความเป็นมาของทฤษฎีบทและความพยายามในการพิสูจน์ ดูตัวอย่าง ). หลังจากเหตุการณ์นี้ บทความทางวิทยาศาสตร์และหนังสือวิทยาศาสตร์ยอดนิยมหลายฉบับปรากฏขึ้นเพื่อสนับสนุนข้อพิสูจน์นี้ แต่ไม่มีผลงานใดที่เปิดเผยข้อผิดพลาดทางคณิตศาสตร์ขั้นพื้นฐานในนั้น ซึ่งไม่ได้พุ่งเข้ามาแม้แต่ความผิดของผู้เขียน แต่เนื่องจากการมองโลกในแง่ดีแปลกๆ บางอย่างที่ครอบงำ ใจนักคณิตศาสตร์ที่ศึกษาปัญหานี้และประเด็นที่เกี่ยวข้อง มีการศึกษาด้านจิตวิทยาของปรากฏการณ์นี้แล้ว. ที่นี่เราให้การวิเคราะห์โดยละเอียดเกี่ยวกับข้อผิดพลาดที่เกิดขึ้น ซึ่งไม่ใช่เรื่องส่วนตัว แต่เป็นผลมาจากความเข้าใจที่ไม่ถูกต้องเกี่ยวกับคุณสมบัติของกำลังของจำนวนเต็ม ดังที่แสดงใน ปัญหาของแฟร์มาต์มีรากฐานมาจากแนวทางเชิงสัจพจน์ใหม่ในการศึกษาคุณสมบัติเหล่านี้ ซึ่งยังไม่ได้นำมาใช้ในวิทยาศาสตร์สมัยใหม่ แต่ข้อพิสูจน์ที่ผิดพลาดกลับขวางทางเขา ทำให้ผู้เชี่ยวชาญด้านทฤษฎีจำนวนได้รับแนวทางที่เป็นเท็จ และนำนักวิจัยชั้นนำเกี่ยวกับปัญหาของแฟร์มาต์ออกห่างจากแนวทางแก้ไขที่ตรงประเด็นและเพียงพอ งานนี้อุทิศตนเพื่อขจัดอุปสรรคนี้

1. กายวิภาคของข้อผิดพลาดที่เกิดขึ้นระหว่างการพิสูจน์ WTF

ในกระบวนการให้เหตุผลที่ยาวนานและน่าเบื่อหน่าย ข้อความดั้งเดิมของแฟร์มาต์ได้รับการปรับปรุงใหม่ในแง่ของการเปรียบเทียบสมการไดโอแฟนไทน์ระดับ pth กับเส้นโค้งวงรีลำดับที่ 3 (ดูทฤษฎีบท 0.4 และ 0.5 นิ้ว) การเปรียบเทียบนี้บังคับให้ผู้เขียนการพิสูจน์โดยรวมต้องประกาศว่าวิธีการและการใช้เหตุผลของพวกเขานำไปสู่การแก้ปัญหาขั้นสุดท้ายของปัญหาของแฟร์มาต์ (จำได้ว่า WTF ไม่ได้รับการยอมรับการพิสูจน์สำหรับกรณีของกำลังจำนวนเต็มตามอำเภอใจจนกระทั่งถึงทศวรรษที่ 90 ของยุคสุดท้าย ศตวรรษ). จุดประสงค์ของการพิจารณานี้คือเพื่อสร้างความไม่ถูกต้องทางคณิตศาสตร์ของการเปรียบเทียบข้างต้น และจากการวิเคราะห์ เพื่อค้นหาข้อผิดพลาดพื้นฐานในการพิสูจน์ที่นำเสนอ

ก) ข้อผิดพลาดเกิดขึ้นที่ไหนและอย่างไร?

ดังนั้นเราจะติดตามข้อความโดยที่ในหน้า 448 ว่ากันว่าหลังจาก "ความคิดที่มีไหวพริบ" ของ G. Frey ความเป็นไปได้ในการพิสูจน์ WTF ก็เปิดออก ในปี 1984 G. Frey เสนอแนะและ

เค. ริเบต์พิสูจน์ในภายหลังว่าเส้นโค้งวงรีสมมุติแทนคำตอบของจำนวนเต็มสมมุติของสมการแฟร์มาต์

y 2 = x(x + ยูพี)(เอ็กซ์ - โวลต์น) (1)

ไม่สามารถเป็นแบบโมดูลาร์ได้ อย่างไรก็ตาม A. Wiles และ R. Taylor พิสูจน์ว่าเส้นโค้งวงรีกึ่งคงที่ทุกเส้นที่กำหนดเหนือสนามจำนวนตรรกยะเป็นแบบโมดูลาร์ สิ่งนี้นำไปสู่ข้อสรุปเกี่ยวกับความเป็นไปไม่ได้ของการแก้จำนวนเต็มของสมการของแฟร์มาต์ และผลที่ตามมาคือความถูกต้องของคำสั่งของแฟร์มาต์ ซึ่งในสัญกรณ์ของ A. Wiles เขียนเป็นทฤษฎีบท 0.5: ให้มีความเท่าเทียมกัน

ยูพี+ โวลต์พี+ วพี = 0 (2)

ที่ไหน ยู, โวลต์, ว- จำนวนตรรกยะ, เลขชี้กำลังจำนวนเต็ม p ≥ 3; ดังนั้น (2) จะพอใจก็ต่อเมื่อ ยูวี = 0 .

เห็นได้ชัดว่า เราควรย้อนกลับไปคิดอย่างมีวิจารณญาณว่าทำไมเส้นโค้ง (1) จึงเป็นนิรนัยที่ถูกมองว่าเป็นรูปวงรี และอะไรคือความเชื่อมโยงที่แท้จริงของมันกับสมการของแฟร์มาต์ เมื่อคาดการณ์ถึงคำถามนี้ A. Wiles อ้างถึงงานของ Y. Hellegouarch ซึ่งเขาพบวิธีที่จะเชื่อมโยงสมการของแฟร์มาต์ (สมมุติว่าแก้ได้เป็นจำนวนเต็ม) กับเส้นโค้งลำดับที่สามสมมุติ ต่างจาก G. Frey ตรงที่ I. Elleguarche ไม่ได้เชื่อมโยงเส้นโค้งของเขากับรูปแบบโมดูลาร์ อย่างไรก็ตาม วิธีการหาสมการ (1) ของเขาถูกนำมาใช้ในการพิสูจน์ของ A. Wiles ต่อไป

มาดูการทำงานกันดีกว่า ผู้เขียนดำเนินการให้เหตุผลในแง่ของเรขาคณิตที่ฉายภาพ เมื่อลดความซับซ้อนของสัญกรณ์บางส่วนและปรับให้สอดคล้องกับ เราพบว่าเส้นโค้งอาบีเลียน

Y 2 = X(X - β p)(X + γ p) (3)

มีการเปรียบเทียบสมการไดโอแฟนไทน์

xพี+ ยพี+ zพี = 0 (4)

ที่ไหน x, ใช่ zเป็นจำนวนเต็มไม่ทราบค่า p คือเลขชี้กำลังจำนวนเต็มจาก (2) และใช้คำตอบของสมการไดโอแฟนไทน์ (4) α p , β p , γ p เพื่อเขียนเส้นโค้งอาบีเลียน (3)

ตอนนี้ เพื่อให้แน่ใจว่านี่คือเส้นโค้งวงรีของลำดับที่ 3 จำเป็นต้องพิจารณาตัวแปร X และ Y ใน (3) ในระนาบแบบยุคลิด ในการทำเช่นนี้ เราใช้กฎเลขคณิตของเส้นโค้งรูปไข่ที่รู้จักกันดี: หากมีจุดตรรกยะสองจุดบนเส้นโค้งพีชคณิตลูกบาศก์และเส้นที่ผ่านจุดเหล่านี้ตัดกับเส้นโค้งนี้ที่จุดอื่น จุดหลังก็เป็นจุดตรรกยะด้วย . สมการสมมุติฐาน (4) เป็นตัวแทนกฎการบวกจุดบนเส้นตรงอย่างเป็นทางการ หากเราทำการเปลี่ยนแปลงตัวแปร xพี = ก, ยพี = ข, z p = C และกำหนดเส้นตรงที่เกิดขึ้นตามแนวแกน X ใน (3) จากนั้นจะตัดเส้นโค้งระดับที่ 3 ที่จุดสามจุด: (X = 0, Y = 0), (X = β p, Y = 0) , (X = - γ p, Y = 0) ซึ่งสะท้อนให้เห็นในสัญกรณ์ของเส้นโค้งอาบีเลียน (3) และสัญกรณ์ที่คล้ายกัน (1) อย่างไรก็ตาม เส้นโค้ง (3) หรือ (1) เป็นรูปวงรีจริงหรือไม่ แน่นอนว่าไม่ เพราะส่วนของเส้นยุคลิดเมื่อเพิ่มจุดเข้าไปนั้นจะถูกถ่ายในระดับที่ไม่เชิงเส้น

เมื่อกลับไปที่ระบบพิกัดเชิงเส้นของปริภูมิแบบยุคลิด เราจะได้สูตร (1) และ (3) ซึ่งแตกต่างจากสูตรสำหรับเส้นโค้งรูปไข่อย่างมาก ตัวอย่างเช่น (1) อาจมีรูปแบบดังต่อไปนี้:

η 2p = ξ p (ξ p + ยูพี)(ξ พี - โวลต์น) (5)

โดยที่ ξ p = x, η p = y และการอุทธรณ์ต่อ (1) ในกรณีนี้เพื่อให้ได้มาซึ่ง WTF ดูเหมือนจะผิดกฎหมาย แม้ว่าข้อเท็จจริงที่ว่า (1) จะเป็นไปตามเกณฑ์บางประการสำหรับคลาสของเส้นโค้งรูปไข่ แต่ก็ไม่เป็นไปตามเกณฑ์ที่สำคัญที่สุดในการเป็นสมการระดับที่ 3 ในระบบพิกัดเชิงเส้น

b) การจำแนกข้อผิดพลาด

กลับมาที่จุดเริ่มต้นของการพิจารณาอีกครั้งเพื่อดูว่าจะได้ข้อสรุปเกี่ยวกับความจริงของ WTF ได้อย่างไร ประการแรก สันนิษฐานว่ามีวิธีแก้สมการของแฟร์มาต์เป็นจำนวนเต็มบวก ประการที่สอง วิธีแก้ปัญหานี้ถูกแทรกลงในรูปแบบพีชคณิตของรูปแบบที่รู้จักโดยพลการ (เส้นโค้งระนาบระดับ 3) ภายใต้สมมติฐานที่ว่าเส้นโค้งรูปไข่ที่ได้รับมีอยู่ (สมมติฐานที่สองที่ไม่ได้รับการยืนยัน) ประการที่สาม เนื่องจากวิธีการอื่นพิสูจน์ว่าเส้นโค้งเฉพาะที่สร้างขึ้นนั้นไม่ใช่แบบโมดูลาร์ นั่นหมายความว่าไม่มีอยู่จริง สิ่งนี้นำไปสู่ข้อสรุป: ไม่มีคำตอบจำนวนเต็มในสมการของแฟร์มาต์ ดังนั้น WTF จึงถูกต้อง

มีลิงก์ที่อ่อนแอจุดหนึ่งในการโต้แย้งเหล่านี้ ซึ่งหลังจากการตรวจสอบโดยละเอียดแล้ว กลายเป็นข้อผิดพลาด ข้อผิดพลาดนี้เกิดขึ้นในขั้นตอนที่สองของกระบวนการพิสูจน์ เมื่อสันนิษฐานว่าคำตอบสมมุติของสมการแฟร์มาต์ก็เป็นคำตอบของสมการพีชคณิตระดับที่ 3 เช่นกัน ซึ่งอธิบายเส้นโค้งวงรีของรูปแบบที่รู้จัก ในตัวมันเอง ข้อสันนิษฐานดังกล่าวจะสมเหตุสมผลหากเส้นโค้งที่ระบุเป็นรูปวงรีจริงๆ อย่างไรก็ตาม ดังที่เห็นได้จากจุด 1a) เส้นโค้งนี้แสดงอยู่ในพิกัดที่ไม่เชิงเส้น ซึ่งทำให้เป็น "ภาพลวงตา" เช่น ไม่มีอยู่ในปริภูมิทอพอโลยีเชิงเส้นจริงๆ

ตอนนี้เราจำเป็นต้องจำแนกข้อผิดพลาดที่พบอย่างชัดเจน มันอยู่ในความจริงที่ว่าสิ่งที่จำเป็นต้องพิสูจน์นั้นถูกนำเสนอเป็นข้อโต้แย้งในการพิสูจน์ ในตรรกะดั้งเดิม ข้อผิดพลาดนี้เรียกว่า "วงจรอุบาทว์" ในกรณีนี้ คำตอบจำนวนเต็มของสมการแฟร์มาต์จะถูกเปรียบเทียบ (เห็นได้ชัดว่า สันนิษฐานว่าไม่ซ้ำกัน) กับเส้นโค้งวงรีที่ไม่มีอยู่จริง และจากนั้นความน่าสมเพชของการให้เหตุผลเพิ่มเติมทั้งหมดจะใช้ในการพิสูจน์ว่าได้รับเส้นโค้งวงรีเฉพาะของรูปแบบนี้ จากการแก้สมการสมมุติของสมการแฟร์มาต์ไม่มีอยู่จริง

เกิดขึ้นได้อย่างไรที่พลาดข้อผิดพลาดเบื้องต้นในงานคณิตศาสตร์ร้ายแรง? สิ่งนี้อาจเกิดขึ้นเนื่องจากความจริงที่ว่ารูปทรงเรขาคณิต "ลวงตา" ประเภทนี้ไม่เคยได้รับการศึกษาทางคณิตศาสตร์มาก่อน แท้จริงแล้ว ใครบ้างที่อาจสนใจในวงกลมสมมติที่ได้รับจากสมการของแฟร์มาต์โดยการแทนที่ตัวแปร x n/2 = A, y n/2 = B, z n/2 = C ท้ายที่สุด สมการของมัน C 2 = A 2 + B 2 ไม่มีคำตอบสำหรับจำนวนเต็ม x, y, z และ n ≥ 3 ในแกนพิกัดไม่เชิงเส้น X และ Y วงกลมดังกล่าวจะอธิบายได้ด้วยสมการที่มีลักษณะคล้ายกันมากกับรูปแบบมาตรฐาน:

Y 2 = - (X - A)(X + B)

โดยที่ A และ B ไม่ใช่ตัวแปรอีกต่อไป แต่เป็นตัวเลขเฉพาะที่กำหนดโดยการทดแทนข้างต้น แต่ถ้าให้ตัวเลข A และ B อยู่ในรูปแบบดั้งเดิม ซึ่งประกอบด้วยลักษณะเชิงกำลัง ความแตกต่างของสัญลักษณ์ในปัจจัยทางด้านขวาของสมการจะดึงดูดสายตาทันที คุณลักษณะนี้ช่วยแยกแยะภาพลวงตาจากความเป็นจริง และเปลี่ยนจากพิกัดไม่เชิงเส้นไปเป็นพิกัดเชิงเส้น ในทางกลับกัน หากเราพิจารณาตัวเลขเป็นตัวดำเนินการเมื่อเปรียบเทียบกับตัวแปร ดังเช่นใน (1) ทั้งคู่จะต้องเป็นปริมาณที่เป็นเนื้อเดียวกัน กล่าวคือ ต้องมีองศาเท่ากัน

ความเข้าใจเรื่องกำลังของตัวเลขในฐานะตัวดำเนินการยังช่วยให้เราเห็นว่าการเปรียบเทียบสมการแฟร์มาต์กับเส้นโค้งวงรีลวงนั้นไม่ได้คลุมเครือ ตัวอย่างเช่น พิจารณาตัวประกอบตัวหนึ่งทางด้านขวาของ (5) แล้วแยกย่อยเป็นตัวประกอบเชิงเส้น p โดยให้จำนวนเชิงซ้อน r โดยที่ r p = 1 (ดูตัวอย่าง):

พี + ยูพี = (ξ + ยู)(ξ + ร ยู)(ξ + r 2 ยู)...(ξ + r p-1 ยู) (6)

จากนั้นรูปแบบ (5) สามารถแสดงเป็นการสลายตัวให้เป็นปัจจัยเฉพาะของจำนวนเชิงซ้อนตามประเภทของเอกลักษณ์พีชคณิต (6) อย่างไรก็ตาม ลักษณะเฉพาะของการสลายตัวดังกล่าวในกรณีทั่วไปยังเป็นที่น่าสงสัย ดังที่ Kummer แสดงไว้ครั้งหนึ่ง .

2. ข้อสรุป

จากการวิเคราะห์ครั้งก่อน พบว่าสิ่งที่เรียกว่าเลขคณิตของเส้นโค้งวงรีไม่สามารถให้ความกระจ่างได้ว่าจะหาข้อพิสูจน์ WTF ได้ที่ไหน หลังเลิกงาน คำกล่าวของแฟร์มาต์ซึ่งถือเป็นบทสรุปของบทความนี้เริ่มถูกมองว่าเป็นเรื่องตลกทางประวัติศาสตร์หรือเรื่องหลอกลวง อย่างไรก็ตามในความเป็นจริงปรากฎว่า Fermat ไม่ใช่คนที่ล้อเล่น แต่เป็นผู้เชี่ยวชาญที่รวมตัวกันในการประชุมทางคณิตศาสตร์ที่ Oberwolfach ในประเทศเยอรมนีในปี 1984 ซึ่ง G. Frey เปล่งเสียงความคิดอันมีไหวพริบของเขา ผลที่ตามมาของคำพูดที่ไม่ระมัดระวังดังกล่าวทำให้คณิตศาสตร์โดยรวมเกือบจะสูญเสียความไว้วางใจจากสาธารณชนซึ่งมีการอธิบายอย่างละเอียดในและซึ่งจำเป็นต้องทำให้เกิดคำถามเกี่ยวกับความรับผิดชอบของสถาบันวิทยาศาสตร์ต่อสังคม การเปรียบเทียบสมการแฟร์มาต์กับเส้นโค้งเฟรย์ (1) ถือเป็น “กุญแจ” ของการพิสูจน์ทั้งหมดของไวล์สเกี่ยวกับทฤษฎีบทของแฟร์มาต์ และหากไม่มีความสอดคล้องกันระหว่างเส้นโค้งแฟร์มาต์กับเส้นโค้งวงรีโมดูลาร์ ก็ไม่มีการพิสูจน์

เมื่อเร็วๆ นี้ มีรายงานทางอินเทอร์เน็ตหลายฉบับปรากฏว่าในที่สุดนักคณิตศาสตร์ที่มีชื่อเสียงบางคนก็ได้ค้นพบข้อพิสูจน์ของไวลส์เกี่ยวกับทฤษฎีบทของแฟร์มาต์ โดยให้เหตุผลในรูปแบบของการคำนวณจุดจำนวนเต็มใหม่ในปริภูมิแบบยุคลิดแบบ "น้อยที่สุด" อย่างไรก็ตาม ไม่มีนวัตกรรมใดสามารถยกเลิกผลลัพธ์แบบคลาสสิกที่มนุษย์ได้รับในวิชาคณิตศาสตร์ โดยเฉพาะอย่างยิ่งความจริงที่ว่าแม้ว่าเลขลำดับใดๆ จะตรงกับอะนาล็อกเชิงปริมาณของมัน แต่ก็ไม่สามารถทดแทนได้ในการดำเนินการเปรียบเทียบตัวเลขกัน และด้วยเหตุนี้ โดยมีข้อสรุปที่หลีกเลี่ยงไม่ได้ตามมาว่าเส้นโค้งเฟรย์ (1) ไม่ได้เป็นทรงรีในตอนแรก กล่าวคือ ไม่ใช่ตามคำจำกัดความ

บรรณานุกรม:

1. Ivliev Yu.A. การสร้างข้อพิสูจน์ดั้งเดิมของทฤษฎีบทสุดท้ายของแฟร์มาต์ขึ้นมาใหม่ - United Scientific Journal (หัวข้อ "คณิตศาสตร์") เมษายน 2549 ฉบับที่ 7 (167) หน้า 3-9 โปรดดูสาขา Praci Lugansk ของ International Academy of Informatization ด้วย กระทรวงศึกษาธิการและวิทยาศาสตร์ของประเทศยูเครน มหาวิทยาลัยแห่งชาติ Skhidnoukransky ตั้งชื่อตาม วี.ดาล. 2549 ฉบับที่ 2 (13) หน้า 19-25.
2. Ivliev Yu.A. การหลอกลวงทางวิทยาศาสตร์ที่ยิ่งใหญ่ที่สุดของศตวรรษที่ 20: "การพิสูจน์" ของทฤษฎีบทสุดท้ายของแฟร์มาต์ - วิทยาศาสตร์ธรรมชาติและวิศวกรรมศาสตร์ (หัวข้อ "ประวัติศาสตร์และวิธีการทางคณิตศาสตร์") สิงหาคม 2550 ฉบับที่ 4 (30) หน้า 34-48
3. เอ็ดเวิร์ด จี. (เอ็ดเวิร์ด เอช.เอ็ม.) ทฤษฎีบทสุดท้ายของแฟร์มาต์ การแนะนำทางพันธุกรรมเกี่ยวกับทฤษฎีจำนวนพีชคณิต ต่อ. จากอังกฤษ แก้ไขโดย บี.เอฟ.สคูเบนโก. อ.: มีร์ 2523, 484 หน้า
4. Hellegouarch Y. Points d´ordre 2p h sur les courbes elliptiques - Acta Arithmetica 1975 XXVI หน้า 253-263
5. Wiles A. เส้นโค้งวงรีโมดูลาร์และทฤษฎีบทสุดท้ายของแฟร์มาต์ - พงศาวดารของคณิตศาสตร์ พฤษภาคม 1995 v.141 ชุดที่สอง หมายเลข 3 หน้า 443-551

ลิงค์บรรณานุกรม

Ivliev Yu.A. หลักฐานเท็จของวิลส์เกี่ยวกับทฤษฎีบทสุดท้ายของเฟอร์มา // การวิจัยขั้นพื้นฐาน – 2551. – ลำดับที่ 3. – หน้า 13-16;
URL: http://fundamental-research.ru/ru/article/view?id=2763 (วันที่เข้าถึง: 09/25/2019) เรานำเสนอนิตยสารที่คุณจัดพิมพ์โดยสำนักพิมพ์ "Academy of Natural Sciences"

ในศตวรรษที่ 17 ปิแอร์ แฟร์มาต์ ทนายความและนักคณิตศาสตร์พาร์ทไทม์อาศัยอยู่ในฝรั่งเศส โดยใช้เวลาว่างหลายชั่วโมงไปกับงานอดิเรกของเขา เย็นวันหนึ่งในฤดูหนาว นั่งข้างเตาผิง เขาหยิบยกข้อความที่น่าสงสัยอย่างหนึ่งจากสาขาทฤษฎีจำนวน ซึ่งต่อมาถูกเรียกว่าทฤษฎีบทอันยิ่งใหญ่ของแฟร์มาต์ บางทีความตื่นเต้นอาจไม่สำคัญนักในแวดวงคณิตศาสตร์หากไม่มีเหตุการณ์ใดเหตุการณ์หนึ่งเกิดขึ้น นักคณิตศาสตร์รายนี้มักใช้เวลาช่วงเย็นศึกษาหนังสือเล่มโปรดของเขาเรื่อง “เลขคณิต” โดยไดโอแฟนทัสแห่งอเล็กซานเดรีย (ศตวรรษที่ 3) ในขณะที่เขียนความคิดที่สำคัญไว้ตรงขอบหนังสือ - ความหายากนี้ได้รับการเก็บรักษาไว้อย่างระมัดระวังโดยลูกชายของเขาเพื่อลูกหลาน ดังนั้น บนขอบกระดาษที่กว้างของหนังสือเล่มนี้ มือของแฟร์มาต์จึงทิ้งข้อความไว้ดังนี้: “ฉันมีหลักฐานที่ค่อนข้างชัดเจน แต่มันใหญ่เกินกว่าจะวางไว้ที่ขอบกระดาษ” การบันทึกนี้เองที่ทำให้เกิดความตื่นเต้นอย่างน่าทึ่งรอบทฤษฎีบทนี้ นักคณิตศาสตร์ไม่สงสัยเลยว่านักวิทยาศาสตร์ผู้ยิ่งใหญ่คนนี้ประกาศว่าเขาได้พิสูจน์ทฤษฎีบทของเขาเองแล้ว คุณอาจถามคำถาม:“ เขาพิสูจน์ได้จริง ๆ หรือมันเป็นเรื่องโกหกซ้ำซากหรืออาจมีเวอร์ชันอื่นที่ว่าทำไมบันทึกนี้ซึ่งไม่อนุญาตให้นักคณิตศาสตร์รุ่นต่อ ๆ ไปนอนหลับอย่างสงบสุขจึงจบลงที่ระยะขอบ หนังสือ?"

แก่นแท้ของทฤษฎีบทอันยิ่งใหญ่

ทฤษฎีบทที่รู้จักกันดีของแฟร์มาต์นั้นเรียบง่ายในสาระสำคัญและอยู่ที่ความจริงที่ว่า หาก n มากกว่าสองเป็นจำนวนบวก สมการ X n + Y n = Z n จะไม่มีคำตอบประเภทศูนย์ภายในกรอบงาน ของจำนวนธรรมชาติ สูตรที่ดูเหมือนเรียบง่ายนี้ปกปิดความซับซ้อนอันเหลือเชื่อ และมีการพิสูจน์ว่าได้ต่อสู้มายาวนานกว่าสามศตวรรษ มีสิ่งแปลกอย่างหนึ่ง - ทฤษฎีบทนี้เกิดช้าเนื่องจากกรณีพิเศษที่มี n = 2 ปรากฏขึ้นเมื่อ 2,200 ปีที่แล้ว - นี่คือทฤษฎีบทพีทาโกรัสที่มีชื่อเสียงไม่น้อย

ควรสังเกตว่าเรื่องราวเกี่ยวกับทฤษฎีบทที่รู้จักกันดีของแฟร์มาต์นั้นให้ความรู้และให้ความบันเทิงอย่างมาก ไม่ใช่เฉพาะสำหรับนักคณิตศาสตร์เท่านั้น สิ่งที่น่าสนใจที่สุดคือวิทยาศาสตร์ไม่ใช่งานสำหรับนักวิทยาศาสตร์ แต่เป็นงานอดิเรกธรรมดาๆ ซึ่งทำให้ชาวนามีความยินดีเป็นอย่างยิ่ง เขายังติดต่อกับนักคณิตศาสตร์และเพื่อนอยู่เสมอ และแบ่งปันความคิด แต่น่าแปลกที่เขาไม่มุ่งมั่นที่จะเผยแพร่ผลงานของตัวเอง

ผลงานของเกษตรกรนักคณิตศาสตร์

ส่วนผลงานของชาวนาเองนั้นถูกค้นพบอย่างแม่นยำในรูปแบบตัวอักษรธรรมดา ในบางแห่งหายไปทั้งหน้า และมีเพียงส่วนการติดต่อทางจดหมายเท่านั้นที่รอดมาได้ สิ่งที่น่าสนใจกว่านั้นคือความจริงที่ว่าเป็นเวลาสามศตวรรษที่นักวิทยาศาสตร์มองหาทฤษฎีบทที่ถูกค้นพบในผลงานของชาวนา

แต่ไม่ว่าใครจะกล้าพิสูจน์ ความพยายามก็ลดลงเหลือ "ศูนย์" เดการ์ตนักคณิตศาสตร์ชื่อดังยังกล่าวหานักวิทยาศาสตร์ว่าโอ้อวด แต่ทั้งหมดนี้กลับกลายเป็นเพียงความอิจฉาที่ธรรมดาที่สุด นอกเหนือจากการสร้างมันขึ้นมาแล้ว ชาวนายังพิสูจน์ทฤษฎีบทของเขาเองอีกด้วย จริงอยู่ พบวิธีแก้ปัญหาสำหรับกรณีที่ n=4 สำหรับกรณีของ n=3 นั้น นักคณิตศาสตร์ออยเลอร์เป็นผู้ค้นพบ

พวกเขาพยายามพิสูจน์ทฤษฎีบทของชาวนาอย่างไร

ในตอนต้นของศตวรรษที่ 19 ทฤษฎีบทนี้ยังคงมีอยู่ นักคณิตศาสตร์พบข้อพิสูจน์ทฤษฎีบทมากมายที่จำกัดจำนวนธรรมชาติไว้ภายในสองร้อยเท่านั้น

และในปี 1909 ได้มีการวางจำนวนเงินที่ค่อนข้างใหญ่ ซึ่งเท่ากับหนึ่งแสนเครื่องหมายของแหล่งกำเนิดภาษาเยอรมัน - และทั้งหมดนี้เพียงเพื่อแก้ไขปัญหาที่เกี่ยวข้องกับทฤษฎีบทนี้ เงินรางวัลนั้นถูกทิ้งไว้โดย Paul Wolfskehl ผู้รักคณิตศาสตร์ผู้มั่งคั่งซึ่งมีพื้นเพมาจากประเทศเยอรมนี อย่างไรก็ตามเขาคือผู้ที่ต้องการ "ฆ่าตัวตาย" แต่ต้องขอบคุณการมีส่วนร่วมในทฤษฎีบทของ Fermer เขาจึงอยากมีชีวิตอยู่ ความตื่นเต้นที่เกิดขึ้นทำให้เกิด "ข้อพิสูจน์" มากมายเต็มมหาวิทยาลัยในเยอรมนี และในหมู่นักคณิตศาสตร์ก็มีชื่อเล่นว่า "ชาวนา" เกิดขึ้น ซึ่งถูกใช้อย่างดูถูกเหยียดหยามเพื่ออธิบายคนที่เพิ่งเริ่มต้นที่มีความทะเยอทะยานซึ่งไม่สามารถให้ข้อพิสูจน์ที่ชัดเจนได้

การคาดเดาของนักคณิตศาสตร์ชาวญี่ปุ่น ยูทากะ ทานิยามะ

การเปลี่ยนแปลงในประวัติศาสตร์ของทฤษฎีบทอันยิ่งใหญ่ไม่ได้ถูกสังเกตจนกระทั่งกลางศตวรรษที่ 20 แต่มีเหตุการณ์ที่น่าสนใจอย่างหนึ่งเกิดขึ้น ในปี 1955 นักคณิตศาสตร์ชาวญี่ปุ่น ยูทากะ ทานิยามะ ซึ่งอายุ 28 ปี ได้แสดงให้โลกเห็นถึงข้อความจากสาขาคณิตศาสตร์ที่แตกต่างไปจากเดิมอย่างสิ้นเชิง - สมมติฐานของเขานั้นล้ำหน้าซึ่งแตกต่างจากของแฟร์มาต์ ซึ่งต่างจากสมมติฐานของแฟร์มาต์ ข้อความระบุว่า: “เส้นโค้งวงรีแต่ละวงสอดคล้องกับรูปร่างโมดูลาร์เฉพาะ” ดูเหมือนเป็นเรื่องไร้สาระสำหรับนักคณิตศาสตร์ทุกคน เช่นเดียวกับความคิดที่ว่าต้นไม้ประกอบด้วยโลหะบางชนิด! สมมติฐานที่ขัดแย้งกันเช่นเดียวกับการค้นพบที่น่าทึ่งและชาญฉลาดอื่น ๆ ส่วนใหญ่ไม่ได้รับการยอมรับเนื่องจากพวกเขายังไม่โตพอกับมัน และยูทากะทานิยามะก็ฆ่าตัวตายในอีกสามปีต่อมาซึ่งเป็นการกระทำที่อธิบายไม่ได้ แต่เหนือสิ่งอื่นใดอาจเป็นเกียรติสำหรับอัจฉริยะซามูไรที่แท้จริง

สมมติฐานนี้ไม่ได้รับการจดจำมาตลอดทศวรรษ แต่ในช่วงอายุเจ็ดสิบมันได้รับความนิยมสูงสุด - ได้รับการยืนยันจากทุกคนที่เข้าใจได้ แต่เช่นเดียวกับทฤษฎีบทของแฟร์มาต์ก็ยังคงไม่ได้รับการพิสูจน์

การคาดเดาของทานิยามะและทฤษฎีบทของแฟร์มาต์เกี่ยวข้องกันอย่างไร

15 ปีต่อมา เหตุการณ์สำคัญเกิดขึ้นในวิชาคณิตศาสตร์ และได้รวมสมมติฐานของทฤษฎีบทของญี่ปุ่นและทฤษฎีบทของแฟร์มาต์ที่มีชื่อเสียงเข้าด้วยกัน เกฮาร์ด เกรย์กล่าวว่าเมื่อการคาดเดาของทานิยามะได้รับการพิสูจน์แล้ว ก็จะมีการพิสูจน์ทฤษฎีบทของแฟร์มาต์ด้วย นั่นคืออย่างหลังเป็นผลมาจากการคาดเดาของ Taniyama และภายในหนึ่งปีครึ่งทฤษฎีบทของ Fermat ได้รับการพิสูจน์โดยศาสตราจารย์ Kenneth Ribet จากมหาวิทยาลัยแห่งแคลิฟอร์เนีย

เมื่อเวลาผ่านไป การถดถอยก็ถูกแทนที่ด้วยความก้าวหน้า และวิทยาศาสตร์ก็ก้าวไปข้างหน้าอย่างรวดเร็ว โดยเฉพาะอย่างยิ่งในสาขาเทคโนโลยีคอมพิวเตอร์ ดังนั้นค่าของ n ก็เริ่มเพิ่มขึ้นเรื่อยๆ

ในช่วงปลายศตวรรษที่ 20 คอมพิวเตอร์ที่ทรงพลังที่สุดตั้งอยู่ในห้องปฏิบัติการทางทหาร มีการเขียนโปรแกรมเพื่อแก้ปัญหาแฟร์มาต์ซึ่งเป็นที่รู้จักกันดี จากความพยายามทั้งหมดพบว่าทฤษฎีบทนี้ถูกต้องสำหรับค่า n, x, y หลายค่า แต่น่าเสียดายที่นี่ไม่ใช่ข้อพิสูจน์ขั้นสุดท้าย เนื่องจากไม่มีข้อมูลเฉพาะเจาะจงเช่นนี้

John Wiles พิสูจน์ทฤษฎีบทอันยิ่งใหญ่ของ Fermat

และในที่สุด เมื่อปลายปี 1994 นักคณิตศาสตร์จากอังกฤษ จอห์น ไวล์ส ได้พบและสาธิตข้อพิสูจน์ที่แน่นอนของทฤษฎีบทเฟอร์เมอร์ที่เป็นที่ถกเถียงกัน จากนั้น หลังจากแก้ไขหลายครั้ง การอภิปรายในประเด็นนี้ก็มาถึงข้อสรุปเชิงตรรกะ

ข้อโต้แย้งถูกตีพิมพ์ในนิตยสารมากกว่าหนึ่งร้อยหน้า! นอกจากนี้ ทฤษฎีบทยังได้รับการพิสูจน์โดยใช้เครื่องมือทางคณิตศาสตร์ชั้นสูงที่ทันสมัยกว่าอีกด้วย และสิ่งที่น่าประหลาดใจก็คือในขณะที่ชาวนาเขียนผลงานของเขา อุปกรณ์ดังกล่าวไม่มีอยู่ในธรรมชาติ กล่าวอีกนัยหนึ่งชายคนนี้ได้รับการยอมรับว่าเป็นอัจฉริยะในสาขานี้ซึ่งไม่มีใครโต้แย้งได้ แม้จะมีทุกสิ่งที่เกิดขึ้น แต่วันนี้คุณสามารถมั่นใจได้ว่าทฤษฎีบทที่นำเสนอของนักวิทยาศาสตร์ผู้ยิ่งใหญ่ชาวนานั้นได้รับการพิสูจน์และพิสูจน์แล้วและไม่ใช่นักคณิตศาสตร์คนเดียวที่มีสามัญสำนึกคนเดียวที่จะเริ่มการอภิปรายในหัวข้อนี้ ซึ่งแม้แต่ผู้คลางแคลงใจที่กระตือรือร้นที่สุดของมวลมนุษยชาติก็เห็นด้วย กับ.

ชื่อเต็มของชายผู้เสนอทฤษฎีบทนี้ในภายหลังคือ ปิแอร์ เดอ แฟร์แมร์ เขามีส่วนร่วมในคณิตศาสตร์สาขาต่างๆ มากมาย แต่น่าเสียดายที่ผลงานส่วนใหญ่ของเขาถูกตีพิมพ์หลังจากที่เขาเสียชีวิตเท่านั้น