Dakle, imamo potencije dvojke. Ako uzmete broj iz donje crte, lako možete pronaći snagu na koju ćete morati podići dva da biste dobili ovaj broj. Na primjer, da biste dobili 16, trebate podići dva na četvrtu potenciju. A da biste dobili 64, trebate podići dva na šestu potenciju. To se vidi iz tablice.

A sada, zapravo, definicija logaritma:

Baza a logaritma od x je potencija na koju a mora biti podignuto da bi se dobio x.

Zapis: log a x = b, gdje je a baza, x argument, b je ono čemu je zapravo jednak logaritam.

Na primjer, 2 3 = 8 ⇒ log 2 8 = 3 (logaritam s bazom 2 od 8 je tri jer je 2 3 = 8). S istim uspjehom, zapišite 2 64 = 6, budući da je 2 6 = 64.

Operacija pronalaženja logaritma broja prema danoj bazi naziva se logaritmiranje. Dakle, dodajmo novi red u našu tablicu:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Nažalost, ne izračunavaju se svi logaritmi tako lako. Na primjer, pokušajte pronaći log 2 5. Broj 5 nije u tablici, ali logika nalaže da će logaritam ležati negdje na intervalu. Jer 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Takvi se brojevi nazivaju iracionalnim: brojevi iza decimalne točke mogu se pisati ad infinitum i nikada se ne ponavljaju. Ako se logaritam pokaže iracionalnim, bolje ga je ostaviti takvim: log 2 5, log 3 8, log 5 100.

Važno je razumjeti da je logaritam izraz s dvije varijable (baza i argument). Mnogi ljudi isprva brkaju gdje je osnova, a gdje argument. Kako biste izbjegli dosadne nesporazume, samo pogledajte sliku:

[Natpis za sliku]

Pred nama je ništa više od definicije logaritma. Zapamtiti: logaritam je potencija, u koju se mora ugraditi baza da bi se dobio argument. To je baza koja je podignuta na potenciju - na slici je označena crvenom bojom. Ispada da je baza uvijek na dnu! Svojim učenicima govorim ovo divno pravilo na prvoj lekciji - i ne dolazi do zabune.

Shvatili smo definiciju - preostaje samo naučiti brojati logaritme, tj. riješite se znaka "log". Za početak napominjemo da iz definicije proizlaze dvije važne činjenice:

1. Argument i baza uvijek moraju biti veći od nule. To proizlazi iz definicije stupnja pomoću racionalnog eksponenta, na koji se svodi definicija logaritma.
2. Baza mora biti drugačija od jedne, budući da jedno u bilo kojem stupnju i dalje ostaje jedno. Zbog toga je besmisleno pitanje "na koju se snagu treba uzdići da bi se dobilo dvoje". Ne postoji takva diploma!

Takva se ograničenja nazivaju raspon prihvatljivih vrijednosti(ODZ). Ispada da ODZ logaritma izgleda ovako: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Imajte na umu da nema ograničenja za broj b (vrijednost logaritma). Na primjer, logaritam može biti negativan: log 2 0,5 = −1, jer 0,5 = 2 −1.

Međutim, sada razmatramo samo numeričke izraze, gdje nije potrebno znati VA logaritma. Sva su ograničenja već uzeta u obzir od strane autora problema. Ali kada logaritamske jednadžbe i nejednadžbe uđu u igru, DL zahtjevi postat će obvezni. Uostalom, osnova i argument mogu sadržavati vrlo jake konstrukcije koje ne moraju nužno odgovarati gornjim ograničenjima.

Sada pogledajmo opću shemu za izračunavanje logaritama. Sastoji se od tri koraka:

1. Izrazite bazu a i argument x kao potenciju s najmanjom mogućom bazom većom od jedan. Usput, bolje je riješiti se decimala;
2. Riješite jednadžbu za varijablu b: x = a b ;
3. Rezultirajući broj b bit će odgovor.

To je sve! Ako se logaritam pokaže iracionalnim, to će biti vidljivo već u prvom koraku. Zahtjev da baza bude veća od jedan vrlo je važan: to smanjuje vjerojatnost pogreške i uvelike pojednostavljuje izračune. Isto je i s decimalnim razlomcima: ako ih odmah pretvorite u obične, bit će puno manje pogrešaka.

Pogledajmo kako ova shema funkcionira koristeći konkretne primjere:

Zadatak. Izračunajte logaritam: log 5 25

1. Zamislimo bazu i argument kao potenciju broja pet: 5 = 5 1 ; 25 = 5 2 ;
2. Kreirajmo i riješimo jednadžbu:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. Dobili smo odgovor: 2.

Zadatak. Izračunajte logaritam:

[Natpis za sliku]

Zadatak. Izračunajte logaritam: log 4 64

1. Zamislimo bazu i argument kao potenciju dvojke: 4 = 2 2 ; 64 = 2 6 ;
2. Kreirajmo i riješimo jednadžbu:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. Dobili smo odgovor: 3.

Zadatak. Izračunajte logaritam: log 16 1

1. Zamislimo bazu i argument kao potenciju dvojke: 16 = 2 4 ; 1 = 20;
2. Kreirajmo i riješimo jednadžbu:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. Dobili smo odgovor: 0.

Zadatak. Izračunajte logaritam: log 7 14

1. Zamislimo bazu i argument kao potenciju broja sedam: 7 = 7 1 ; 14 se ne može predstaviti kao stepen od sedam, budući da je 7 1< 14 < 7 2 ;
2. Iz prethodnog odlomka proizlazi da se logaritam ne računa;
3. Odgovor je bez promjene: log 7 14.

Mala napomena o posljednjem primjeru. Kako možete biti sigurni da broj nije točna potencija drugog broja? Vrlo je jednostavno - samo ga rastavite na proste faktore. A ako se takvi faktori ne mogu sakupiti u potencije s istim eksponentima, tada izvorni broj nije točna potencija.

Zadatak. Utvrdite jesu li brojevi točne potencije: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 - točan stupanj, jer postoji samo jedan množitelj;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nije točna potencija, jer postoje dva faktora: 3 i 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - točan stupanj;
35 = 7 · 5 - opet nije točna potencija;
14 = 7 · 2 - opet nije točan stupanj;

Primijetite također da su sami prosti brojevi uvijek sami sebi točne potencije.

Decimalni logaritam

Neki logaritmi su toliko uobičajeni da imaju poseban naziv i simbol.

Decimalni logaritam od x je logaritam na bazi 10, tj. Potencija na koju treba podići broj 10 da bi se dobio broj x. Oznaka: lg x.

Na primjer, log 10 = 1; lg 100 = 2; lg 1000 = 3 - itd.

Od sada, kada se u udžbeniku pojavi fraza poput "Pronađi lg 0,01", znajte da to nije tipfeler. Ovo je decimalni logaritam. Međutim, ako niste upoznati s ovim zapisom, uvijek ga možete prepisati:
log x = log 10 x

Sve što vrijedi za obične logaritme vrijedi i za decimalne logaritme.

Prirodni logaritam

Postoji još jedan logaritam koji ima svoju oznaku. Na neki način, to je čak i važnije od decimalnog broja. Govorimo o prirodnom logaritmu.

Prirodni logaritam od x je logaritam prema bazi e, tj. potenciju na koju treba podići broj e da bi se dobio broj x. Oznaka: ln x .

Mnogi će se upitati: što je broj e? Ovo je iracionalan broj, njegova točna vrijednost se ne može pronaći i zapisati. Navest ću samo prve brojke:
e = 2,718281828459...

Nećemo ulaziti u detalje o tome koji je to broj i zašto je potreban. Samo zapamtite da je e baza prirodnog logaritma:
ln x = log e x

Stoga je ln e = 1; ln e 2 = 2; U 16 = 16 - itd. S druge strane, ln 2 je iracionalan broj. Općenito, prirodni logaritam svakog racionalnog broja je iracionalan. Osim, naravno, jednog: ln 1 = 0.

Za prirodne logaritme vrijede sva pravila koja vrijede za obične logaritme.

Logaritam danog broja naziva se eksponent na koji se mora povisiti drugi broj, tzv osnova logaritam da dobijemo ovaj broj. Na primjer, logaritam baze 10 od 100 je 2. Drugim riječima, 10 se mora kvadrirati da bi se dobilo 100 (10 2 = 100). Ako n– određeni broj, b– baza i l– logaritam, dakle b l = n. Broj n također se naziva bazni antilogaritam b brojevima l. Na primjer, antilogaritam od 2 na bazu 10 jednak je 100. To se može napisati u obliku logaritma odnosa b n = l i antilog b l = n.

Osnovna svojstva logaritama:

Svaki pozitivan broj osim jedan može poslužiti kao baza za logaritme, ali nažalost ispada da ako b I n su racionalni brojevi, onda u rijetkim slučajevima postoji takav racionalan broj l, Što b l = n. Međutim, moguće je definirati iracionalan broj l, na primjer, tako da je 10 l= 2; ovo je iracionalan broj l može se aproksimirati s bilo kojom potrebnom točnošću racionalnim brojevima. Pokazuje se da u navedenom primjeru l približno je jednako 0,3010, a ova aproksimacija logaritma s bazom 10 od 2 može se pronaći u četveroznamenkastim tablicama decimalnih logaritama. Logaritmi baze 10 (ili logaritmi baze 10) toliko se često koriste u izračunima da se nazivaju obični logaritmi i zapisani kao log2 = 0,3010 ili log2 = 0,3010, izostavljajući eksplicitnu indikaciju baze logaritma. Logaritmi prema bazi e, transcendentni broj približno jednak 2,71828, nazivaju se prirodni logaritmi. Nalaze se uglavnom u djelima o matematičkoj analizi i njezinoj primjeni u različitim znanostima. Prirodni logaritmi se također pišu bez eksplicitnog označavanja baze, ali koristeći posebnu oznaku ln: na primjer, ln2 = 0,6931, jer e 0,6931 = 2.

Korištenje tablica običnih logaritama.

Pravilni logaritam broja je eksponent na koji se mora podići 10 da bi se dobio zadani broj. Kako je 10 0 = 1, 10 1 = 10 i 10 2 = 100, odmah dobivamo da je log1 = 0, log10 = 1, log100 = 2 itd. za rastuće cjelobrojne potencije 10. Isto tako, 10 –1 = 0,1, 10 –2 = 0,01 i prema tome log0,1 = –1, log0,01 = –2, itd. za sve negativne cijele potencije 10. Uobičajeni logaritmi preostalih brojeva zatvoreni su između logaritama najbližih cijelih potencija od 10; log2 mora biti između 0 i 1, log20 mora biti između 1 i 2, a log0.2 mora biti između -1 i 0. Dakle, logaritam se sastoji od dva dijela, cijelog broja i decimale, okruženih između 0 i 1. cjelobrojni dio tzv karakteristika logaritam i određuje se samim brojem, razlomački dio se zove kazaljka a mogu se pronaći iz tablica. Također, log20 = log(2g̀10) = log2 + log10 = (log2) + 1. Logaritam od 2 je 0,3010, pa je log20 = 0,3010 + 1 = 1,3010. Slično, log0,2 = log(2o10) = log2 – log10 = (log2) – 1 = 0,3010 – 1. Nakon oduzimanja dobivamo log0,2 = – 0,6990. Međutim, praktičnije je predstaviti log0,2 kao 0,3010 – 1 ili kao 9,3010 – 10; Može se formulirati i opće pravilo: svi brojevi dobiveni iz zadanog broja množenjem potencijom broja 10 imaju identične mantise jednake mantisi zadanog broja. Većina tablica prikazuje mantise brojeva u rasponu od 1 do 10, budući da se mantise svih ostalih brojeva mogu dobiti iz onih danih u tablici.

Većina tablica daje logaritme s četiri ili pet decimala, iako postoje tablice sa sedam znamenki i tablice s još više decimala. Najlakši način da naučite kako koristiti takve tablice je na primjerima. Da bismo pronašli log3.59, prije svega, uočimo da je broj 3.59 između 10 0 i 10 1, pa je njegova karakteristika 0. U tablici nalazimo broj 35 (lijevo) i krećemo se duž retka do stupac koji ima broj 9 na vrhu; sjecište ovog stupca i retka 35 je 5551, pa je log3,59 = 0,5551. Da biste pronašli mantisu broja s četiri značajne znamenke, morate koristiti interpolaciju. U nekim tablicama, interpolacija je olakšana omjerima danim u zadnjih devet stupaca na desnoj strani svake stranice tablice. Pronađimo sada log736.4; broj 736.4 nalazi se između 10 2 i 10 3, stoga je karakteristika njegovog logaritma 2. U tablici nalazimo redak lijevo od kojeg je 73 i stupac 6. Na sjecištu ovog retka i ovog stupca nalazi se broj 8669. Među linearnim dijelovima nalazimo stupac 4. Na sjecištu retka 73 i stupca 4 nalazi se broj 2. Dodavanjem 2 na 8669 dobivamo mantisu - jednaka je 8671. Dakle, log736.4 = 2.8671.

Prirodni logaritmi.

Tablice i svojstva prirodnih logaritama slični su tablicama i svojstvima običnih logaritama. Glavna razlika između oba je u tome što cjelobrojni dio prirodnog logaritma nije značajan u određivanju položaja decimalne točke, pa stoga razlika između mantise i karakteristike ne igra posebnu ulogu. Prirodni logaritmi brojeva 5,432; 54,32 i 543,2 jednako su 1,6923; 3,9949 i 6,2975. Odnos između ovih logaritama postat će očit ako uzmemo u obzir razlike između njih: log543.2 – log54.32 = 6.2975 – 3.9949 = 2.3026; posljednji broj nije ništa više od prirodnog logaritma broja 10 (napisano ovako: ln10); log543,2 – log5,432 = 4,6052; posljednji broj je 2ln10. Ali 543,2 = 10g54,32 = 10 2g5,432. Dakle, prirodnim logaritmom danog broja a možete pronaći prirodne logaritme brojeva jednake umnošcima broja a za bilo koju diplomu n brojevi 10 ako do ln a dodajte ln10 pomnoženo s n, tj. ln( aґ10n) = log a + n ln10 = ln a + 2,3026n. Na primjer, ln0,005432 = ln(5,432g̀10 –3) = ln5,432 – 3ln10 = 1,6923 – (3g̀2,3026) = – 5,2155. Stoga tablice prirodnih logaritama, kao i tablice običnih logaritama, obično sadrže samo logaritme brojeva od 1 do 10. U sustavu prirodnih logaritama može se govoriti o antilogaritmima, ali se češće govori o eksponencijalnoj funkciji ili eksponentu. Ako x= log g, To g = e x, I g naziva eksponent od x(radi tipografske pogodnosti često pišu g= eksp x). Eksponent ima ulogu antilogaritma broja x.

Koristeći tablice decimalnih i prirodnih logaritama, možete izraditi tablice logaritama u bilo kojoj bazi osim 10 i e. Ako log b a = x, To b x = a, a time i log c b x= log c a ili x log c b= log c a, ili x= log c a/log c b= log b a. Stoga, koristeći ovu formulu inverzije iz tablice osnovnog logaritma c možete napraviti tablice logaritama u bilo kojoj drugoj bazi b. Množitelj 1/log c b nazvao prijelazni modul iz baze c do baze b. Ništa ne sprječava, na primjer, korištenje formule inverzije ili prijelaz iz jednog sustava logaritama u drugi, pronalaženje prirodnih logaritama iz tablice običnih logaritama ili pravljenje obrnutog prijelaza. Na primjer, log105.432 = log e 5.432/log e 10 = 1,6923/2,3026 = 1,6923g0,4343 = 0,7350. Broj 0,4343, kojim treba pomnožiti prirodni logaritam određenog broja da bi se dobio obični logaritam, je modul prijelaza u sustav običnih logaritama.

Posebne tablice.

Logaritmi su izvorno izmišljeni tako da se pomoću njihovih svojstava log ab= log a+ log b i log a/b= log a–log b, pretvaraju umnoške u zbrojeve, a količnike u razlike. Drugim riječima, ako log a i log b poznati, tada pomoću zbrajanja i oduzimanja možemo lako pronaći logaritam umnoška i kvocijenta. U astronomiji se, međutim, često daju vrijednosti log a i log b treba pronaći dnevnik( a + b) ili log( a – b). Naravno, prvo se može pronaći iz tablica logaritama a I b, zatim izvršite naznačeno zbrajanje ili oduzimanje i opet pozivajući se na tablice pronađite tražene logaritme, ali bi takav postupak zahtijevao tri puta pozivanje na tablice. Z. Leonelli 1802. godine objavio je tablice tzv. Gaussovi logaritmi– logaritmi za zbrajanje zbrojeva i razlika – što je omogućilo ograničiti se na jedan pristup tablicama.

Godine 1624. I. Kepler je predložio tablice proporcionalnih logaritama, t j . logaritmi brojeva a/x, Gdje a– neka pozitivna konstantna vrijednost. Ove tablice prvenstveno koriste astronomi i navigatori.

Proporcionalni logaritmi pri a= 1 nazivaju se kologaritmi a koriste se u izračunima kada treba raditi s umnošcima i kvocijentima. Kologaritam broja n jednak logaritmu recipročnog broja; oni. colog n= log1/ n= – log n. Ako je log2 = 0,3010, tada je colog2 = – 0,3010 = 0,6990 – 1. Prednost korištenja kologaritama je u tome što pri izračunavanju vrijednosti logaritma izraza poput pq/r trostruki zbroj pozitivnih decimala log str+ log q+kolog r je lakše pronaći nego mješoviti dnevnik zbroja i razlike str+ log q–log r.

Priča.

Načelo na kojem se temelji bilo koji sustav logaritama poznato je jako dugo i može se pratiti sve do drevne babilonske matematike (oko 2000. pr. Kr.). U to se vrijeme interpolacija između tabličnih vrijednosti pozitivnih cijelih potencija cijelih brojeva koristila za izračunavanje složenih kamata. Mnogo kasnije, Arhimed (287. – 212. pr. Kr.) upotrijebio je potencije od 108 kako bi pronašao gornju granicu broja zrnaca pijeska potrebnih da se potpuno ispuni tada poznati Svemir. Arhimed je skrenuo pozornost na svojstvo eksponenata koje je u osnovi učinkovitosti logaritama: umnožak potencija odgovara zbroju eksponenata. Krajem srednjeg vijeka i početkom modernog doba matematičari su se sve više počeli okretati odnosu između geometrijskih i aritmetičkih progresija. M. Stiefel u svom eseju Aritmetika cijelog broja(1544) dao je tablicu pozitivnih i negativnih snaga broja 2:

Stiefel je primijetio da je zbroj dva broja u prvom redu (red eksponenta) jednak eksponentu dva koji odgovara umnošku dvaju odgovarajućih brojeva u donjem redu (red eksponenta). U vezi s ovom tablicom Stiefel je formulirao četiri pravila koja su ekvivalentna četirima modernim pravilima za operacije s eksponentima ili četirima pravilima za operacije s logaritmima: zbroj u gornjem retku odgovara umnošku na donjem retku; oduzimanje u gornjoj liniji odgovara dijeljenju u donjoj liniji; množenje u gornjoj liniji odgovara potenciranju u donjoj liniji; podjela na gornjoj liniji odgovara ukorjenjivanju na donjoj liniji.

Očigledno su pravila slična Stiefelovim pravilima navela J. Napera da formalno uvede prvi sustav logaritama u svom radu Opis nevjerojatne tablice logaritama, objavljen 1614. Ali Napierove misli bile su zaokupljene problemom pretvaranja umnožaka u zbrojeve otkad je, više od deset godina prije objavljivanja njegova rada, Napier primio vijest iz Danske da na zvjezdarnici Tycho Brahe njegovi pomoćnici imaju metodu koja omogućuje moguće je umnoške pretvoriti u zbrojeve. Metoda o kojoj se raspravljalo u poruci koju je Napier primio temeljila se na upotrebi trigonometrijskih formula poput

stoga su se Naperove tablice sastojale uglavnom od logaritama trigonometrijskih funkcija. Iako pojam baze nije izričito uključen u definiciju koju je predložio Napier, ulogu ekvivalentnu bazi sustava logaritama u njegovom sustavu imao je broj (1 – 10 –7)g10 7, približno jednak 1/ e.

Neovisno o Naperu i gotovo istodobno s njim, J. Bürgi u Pragu izumio je i objavio sustav logaritama, vrlo sličan po vrsti, objavljen 1620. Tablice aritmetičke i geometrijske progresije. To su bile tablice antilogaritama prema bazi (1 + 10 –4) ´10 4, prilično dobra aproksimacija broja e.

U Naperovom sustavu logaritam broja 10 7 uzet je kao nula, a kako su se brojevi smanjivali, logaritmi su rasli. Kad je G. Briggs (1561. – 1631.) posjetio Napier, obojica su se složila da bi bilo prikladnije koristiti broj 10 kao bazu, a logaritam od jedan smatrati nulom. Zatim, kako su brojevi rasli, njihovi logaritmi bi se povećavali. Tako smo dobili moderni sustav decimalnih logaritama čiju je tablicu Briggs objavio u svom djelu Logaritamska aritmetika(1620). Logaritmi prema bazi e, iako ne baš one koje je uveo Naper, često se nazivaju Naperovim. Termine "karakteristika" i "mantisa" predložio je Briggs.

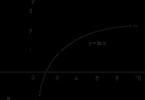
Prvi logaritmi su iz povijesnih razloga koristili aproksimacije brojeva 1/ e I e. Nešto kasnije, ideja o prirodnim logaritmima počela se povezivati ​​s proučavanjem područja pod hiperbolom xy= 1 (slika 1). U 17. stoljeću pokazalo se da područje omeđeno ovom krivuljom, os x i ordinate x= 1 i x = a(na slici 1 ovo je područje prekriveno masnijim i rijetkim točkama) povećava aritmetičku progresiju kada a raste eksponencijalno. Upravo se ta ovisnost javlja u pravilima za rad s eksponentima i logaritmima. To je dovelo do toga da se Naperianovi logaritmi nazovu "hiperboličnim logaritmima".

Logaritamska funkcija.

Postojalo je vrijeme kada su se logaritmi smatrali isključivo sredstvom izračuna, ali u 18. stoljeću, uglavnom zahvaljujući radu Eulera, formiran je koncept logaritamske funkcije. Graf takve funkcije g= log x, čije ordinate rastu u aritmetičkoj progresiji, dok apscise rastu u geometrijskoj progresiji, prikazan je na sl. 2, A. Graf inverzne ili eksponencijalne funkcije y = e x, čije se ordinate povećavaju u geometrijskoj progresiji, a čije apscise rastu u aritmetičkoj progresiji, prikazano je redom na sl. 2, b. (Krivulje g= log x I g = 10x oblikom sličan krivuljama g= log x I g = e x.) Također su predložene alternativne definicije logaritamske funkcije, npr.

kpi; i, slično tome, prirodni logaritmi broja -1 su kompleksni brojevi oblika (2 k + 1)pi, Gdje k– cijeli broj. Slične izjave vrijede za opće logaritme ili druge sustave logaritama. Dodatno, definicija logaritama može se generalizirati korištenjem Eulerovih identiteta kako bi se uključili kompleksni logaritmi kompleksnih brojeva.

Alternativnu definiciju logaritamske funkcije daje funkcionalna analiza. Ako f(x) – kontinuirana funkcija realnog broja x, koji ima sljedeća tri svojstva: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), To f(x) definiran je kao logaritam broja x na temelju b. Ova definicija ima brojne prednosti u odnosu na definiciju danu na početku ovog članka.

Prijave.

Logaritmi su se izvorno koristili isključivo za pojednostavljenje izračuna, a ova im je primjena još uvijek jedna od najvažnijih. Izračunavanje umnožaka, kvocijenata, potencija i korijena olakšano je ne samo širokom dostupnošću objavljenih tablica logaritama, već i korištenjem tzv. klizač - računalni alat čiji se princip rada temelji na svojstvima logaritama. Ravnalo je opremljeno logaritamskim skalama, tj. udaljenost od broja 1 do bilo kojeg broja x izabran da bude jednak log x; Pomicanjem jedne ljestvice u odnosu na drugu moguće je crtati zbrojeve ili razlike logaritama, što omogućuje direktno očitavanje umnožaka ili kvocijenata odgovarajućih brojeva s ljestvice. Također možete iskoristiti prednosti predstavljanja brojeva u logaritamskom obliku. logaritamski papir za crtanje grafikona (papir s otisnutim logaritamskim mjerilima na obje koordinatne osi). Ako funkcija zadovoljava potencijski zakon oblika y = kxn, tada njegov logaritamski grafikon izgleda kao ravna linija, jer log g= log k + n log x– jednadžba linearna u odnosu na log g i log x. Naprotiv, ako logaritamski graf neke funkcionalne ovisnosti izgleda kao ravna linija, tada je ta ovisnost potencna. Polu-log papir (gdje os y ima logaritamsko mjerilo, a os x jednoliko mjerilo) koristan je kada trebate identificirati eksponencijalne funkcije. Jednadžbe oblika y = kb rx događaju kad god se količina, kao što je broj stanovnika, količina radioaktivnog materijala ili bankovni saldo, smanjuje ili povećava po stopi proporcionalnoj količini stanovništva, radioaktivnog materijala ili trenutno dostupnog novca. Ako se takva ovisnost iscrta na polulogaritamskom papiru, graf će izgledati kao ravna crta.

Logaritamska funkcija nastaje u vezi s velikim brojem prirodnih oblika. Cvjetovi u cvatovima suncokreta raspoređeni su u logaritamske spirale, ljušture mekušaca su uvijene Nautilus, rogove planinske ovce i kljunove papiga. Svi ovi prirodni oblici mogu poslužiti kao primjeri krivulje poznate kao logaritamska spirala jer je u polarnom koordinatnom sustavu njezina jednadžba r = ae bq, ili ln r= log a + bq. Takvu krivulju opisuje pomična točka čija se udaljenost od pola povećava u geometrijskoj progresiji, a kut opisan njezinim radijus vektorom raste u aritmetičkoj progresiji. Sveprisutnost takve krivulje, a time i logaritamske funkcije, dobro je ilustrirana činjenicom da se pojavljuje u tako udaljenim i potpuno različitim područjima kao što su kontura ekscentričnog brijega i putanja nekih insekata koji lete prema svjetlu.

Kao što znate, kod množenja izraza s potencijama, njihovi eksponenti uvijek se zbrajaju (a b *a c = a b+c). Taj je matematički zakon izveo Arhimed, a kasnije, u 8. stoljeću, matematičar Virasen izradio je tablicu cjelobrojnih eksponenata. Upravo su oni poslužili za daljnje otkriće logaritama. Primjeri korištenja ove funkcije mogu se naći gotovo posvuda gdje trebate pojednostaviti glomazno množenje jednostavnim zbrajanjem. Ako provedete 10 minuta čitajući ovaj članak, objasnit ćemo vam što su logaritmi i kako s njima raditi. Jednostavnim i pristupačnim jezikom.

Definicija u matematici

Logaritam je izraz sljedećeg oblika: log a b=c, to jest, logaritam bilo kojeg nenegativnog broja (to jest, bilo kojeg pozitivnog) "b" na njegovu bazu "a" smatra se potencijom "c ” na koju se mora podići baza “a” da bi se u konačnici dobila vrijednost “b”. Analizirajmo logaritam koristeći primjere, recimo da postoji izraz log 2 8. Kako pronaći odgovor? Vrlo je jednostavno, trebate pronaći takvu potenciju da od 2 do tražene potencije dobijete 8. Nakon što malo izračunate u glavi, dobivamo broj 3! I to je istina, jer 2 na potenciju 3 daje odgovor kao 8.

Vrste logaritama

Za mnoge učenike i studente ova se tema čini kompliciranom i nerazumljivom, ali zapravo logaritmi nisu tako strašni, glavna stvar je razumjeti njihovo opće značenje i zapamtiti njihova svojstva i neka pravila. Postoje tri odvojene vrste logaritamskih izraza:

1. Prirodni logaritam ln a, gdje je baza Eulerov broj (e = 2,7).
2. Decimala a, gdje je baza 10.
3. Logaritam bilo kojeg broja b na bazu a>1.

Svaki od njih rješava se na standardni način, uključujući pojednostavljenje, redukciju i naknadnu redukciju na jedan logaritam pomoću logaritamskih teorema. Da biste dobili točne vrijednosti logaritama, trebali biste se sjetiti njihovih svojstava i slijeda radnji prilikom njihovog rješavanja.

Pravila i neka ograničenja

U matematici postoji nekoliko pravila-ograničenja koja su prihvaćena kao aksiom, odnosno ne podliježu raspravi i istinita su. Na primjer, nemoguće je podijeliti brojeve s nulom, a također je nemoguće izvući parni korijen negativnih brojeva. Logaritmi također imaju svoja pravila, nakon kojih možete lako naučiti raditi čak i s dugim i prostranim logaritamskim izrazima:

• Baza "a" uvijek mora biti veća od nule, a ne jednaka 1, inače će izraz izgubiti svoje značenje, jer su "1" i "0" u bilo kojem stupnju uvijek jednake svojim vrijednostima;
• ako je a > 0, tada je a b >0, ispada da i “c” mora biti veće od nule.

Kako riješiti logaritme?

Na primjer, dan je zadatak pronaći odgovor na jednadžbu 10 x = 100. To je vrlo jednostavno, potrebno je odabrati potenciju dizanjem broja deset na koji dobijemo 100. To je, naravno, 10 2 = 100.

Sada predstavimo ovaj izraz u logaritamskom obliku. Dobivamo log 10 100 = 2. Kod rješavanja logaritama sve radnje praktički konvergiraju da se nađe potencija kojoj je potrebno unijeti bazu logaritma da bi se dobio zadani broj.

Da biste točno odredili vrijednost nepoznatog stupnja, morate naučiti kako raditi s tablicom stupnjeva. Ovako izgleda:

Kao što vidite, neke eksponente možete pogoditi intuitivno ako imate tehnički um i znanje o tablici množenja. Međutim, za veće vrijednosti trebat će vam tablica snage. Mogu ga koristiti čak i oni koji ne znaju baš ništa o složenim matematičkim temama. Lijevi stupac sadrži brojeve (baza a), gornji red brojeva je vrijednost potencije c na koju je podignut broj a. Na raskrižju ćelije sadrže brojčane vrijednosti koje su odgovor (a c =b). Uzmimo, na primjer, prvu ćeliju s brojem 10 i kvadriramo je, dobivamo vrijednost 100, koja je naznačena na sjecištu naše dvije ćelije. Sve je tako jednostavno i lako da će i najveći humanist razumjeti!

Jednadžbe i nejednadžbe

Ispada da je pod određenim uvjetima eksponent logaritam. Stoga se svaki matematički numerički izraz može napisati kao logaritamska jednakost. Na primjer, 3 4 =81 može se napisati kao logaritam baze 3 od 81 jednak četiri (log 3 81 = 4). Za negativne potencije pravila su ista: 2 -5 = 1/32 zapisujemo kao logaritam, dobivamo log 2 (1/32) = -5. Jedan od najfascinantnijih dijelova matematike je tema "logaritmi". U nastavku ćemo pogledati primjere i rješenja jednadžbi, odmah nakon proučavanja njihovih svojstava. Sada pogledajmo kako nejednadžbe izgledaju i kako ih razlikovati od jednadžbi.

Zadan je sljedeći izraz: log 2 (x-1) > 3 - to je logaritamska nejednakost, budući da je nepoznata vrijednost “x” ispod logaritamskog znaka. Također se u izrazu uspoređuju dvije količine: logaritam željenog broja na osnovicu dva veći je od broja tri.

Najvažnija razlika između logaritamskih jednadžbi i nejednadžbi je u tome što jednadžbe s logaritmima (na primjer, logaritam 2 x = √9) podrazumijevaju jednu ili više specifičnih brojčanih vrijednosti u odgovoru, dok pri rješavanju nejednadžbe oba raspona prihvatljivih vrijednosti​​i točke se određuju razbijanjem ove funkcije. Kao posljedica toga, odgovor nije jednostavan skup pojedinačnih brojeva, kao u odgovoru na jednadžbu, već kontinuirani niz ili skup brojeva.

Osnovni teoremi o logaritmima

Prilikom rješavanja primitivnih zadataka pronalaženja vrijednosti logaritma, njegova svojstva možda neće biti poznata. Međutim, kada su u pitanju logaritamske jednadžbe ili nejednadžbe, prije svega, potrebno je jasno razumjeti i u praksi primijeniti sva osnovna svojstva logaritama. Kasnije ćemo pogledati primjere jednadžbi; pogledajmo prvo svako svojstvo detaljnije.

1. Glavni identitet izgleda ovako: a logaB =B. Primjenjuje se samo kada je a veće od 0, nije jednako jedan, a B je veće od nule.
2. Logaritam umnoška može se prikazati sljedećom formulom: log d (s 1 * s 2) = log d s 1 + log d s 2. U ovom slučaju, obavezni uvjet je: d, s 1 i s 2 > 0; a≠1. Možete dati dokaz za ovu logaritamsku formulu, s primjerima i rješenjem. Neka je log a s 1 = f 1 i log a s 2 = f 2, tada je a f1 = s 1, a f2 = s 2. Dobivamo da je s 1 * s 2 = a f1 *a f2 = a f1+f2 (svojstva od stupnjeva ), a zatim po definiciji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, što je i trebalo dokazati.
3. Logaritam kvocijenta izgleda ovako: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Teorem u obliku formule ima sljedeći oblik: log a q b n = n/q log a b.

Ova se formula naziva "svojstvo stupnja logaritma". Sliči svojstvima običnih stupnjeva, što i ne čudi, jer se sva matematika temelji na prirodnim postulatima. Pogledajmo dokaz.

Neka je log a b = t, ispada da je a t =b. Podignemo li oba dijela na potenciju m: a tn = b n ;

ali budući da je a tn = (a q) nt/q = b n, stoga je log a q b n = (n*t)/t, tada je log a q b n = n/q log a b. Teorem je dokazan.

Primjeri problema i nejednakosti

Najčešći tipovi zadataka o logaritmima su primjeri jednadžbi i nejednadžbi. Nalaze se u gotovo svim knjigama zadataka, a također su obavezan dio ispita iz matematike. Da biste ušli na sveučilište ili položili prijemni ispit iz matematike, morate znati kako ispravno riješiti takve zadatke.

Nažalost, ne postoji jedinstven plan ili shema za rješavanje i određivanje nepoznate vrijednosti logaritma, ali se određena pravila mogu primijeniti na svaku matematičku nejednadžbu ili logaritamsku jednadžbu. Prije svega, trebali biste saznati može li se izraz pojednostaviti ili svesti na opći oblik. Duge logaritamske izraze možete pojednostaviti ako ispravno koristite njihova svojstva. Brzo ih upoznajmo.

Kada rješavamo logaritamske jednadžbe, moramo odrediti koju vrstu logaritma imamo: primjer izraza može sadržavati prirodni logaritam ili decimalni.

Evo primjera ln100, ln1026. Njihovo se rješenje svodi na to da trebaju odrediti potenciju kojoj će baza 10 biti jednaka 100, odnosno 1026. Za rješavanje prirodnih logaritama morate primijeniti logaritamske identitete ili njihova svojstva. Pogledajmo primjere rješavanja logaritamskih problema raznih vrsta.

Kako koristiti logaritamske formule: s primjerima i rješenjima

Dakle, pogledajmo primjere korištenja osnovnih teorema o logaritmima.

1. Svojstvo logaritma umnoška može se koristiti u zadacima gdje je potrebno veliku vrijednost broja b rastaviti na jednostavnije faktore. Na primjer, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odgovor je 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kao što vidite, koristeći četvrto svojstvo potencije logaritma uspjeli smo riješiti naizgled složen i nerješiv izraz. Samo trebate faktorizirati bazu, a zatim uzeti vrijednosti eksponenta iz znaka logaritma.

Zadaci s jedinstvenog državnog ispita

Logaritmi se često nalaze na prijemnim ispitima, osobito mnogi logaritamski problemi na Jedinstvenom državnom ispitu (državni ispit za sve maturante). Obično su ti zadaci prisutni ne samo u dijelu A (najlakši ispitni dio ispita), već i u dijelu C (najsloženiji i najobimniji zadaci). Ispit zahtijeva točno i savršeno poznavanje teme “Prirodni logaritmi”.

Primjeri i rješenja problema preuzeti su iz službenih verzija Jedinstvenog državnog ispita. Pogledajmo kako se takvi zadaci rješavaju.

Zadani je log 2 (2x-1) = 4. Rješenje:
prepišimo izraz, malo ga pojednostavimo log 2 (2x-1) = 2 2, po definiciji logaritma dobivamo da je 2x-1 = 2 4, dakle 2x = 17; x = 8,5.

• Najbolje je svesti sve logaritme na istu bazu kako rješenje ne bi bilo glomazno i ​​zbunjujuće.
• Svi izrazi pod znakom logaritma označeni su kao pozitivni, stoga, kada se eksponent izraza koji je pod znakom logaritma i kao njegova baza izuzme kao množitelj, izraz koji ostaje ispod logaritma mora biti pozitivan.

Održavanje vaše privatnosti važno nam je. Iz tog razloga razvili smo Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte naše prakse privatnosti i javite nam ako imate bilo kakvih pitanja.

Prikupljanje i korištenje osobnih podataka

Osobni podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da date svoje osobne podatke u bilo kojem trenutku kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta osobnih podataka koje možemo prikupljati i kako možemo koristiti takve podatke.

Koje osobne podatke prikupljamo:

• Kada podnesete prijavu na stranici, možemo prikupiti razne informacije, uključujući vaše ime, telefonski broj, adresu e-pošte itd.

Kako koristimo vaše osobne podatke:

• Osobni podaci koje prikupljamo omogućuju nam da vas kontaktiramo s jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše osobne podatke za slanje važnih obavijesti i komunikacija.
• Također možemo koristiti osobne podatke u interne svrhe, kao što je provođenje revizija, analiza podataka i raznih istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
• Ako sudjelujete u izvlačenju nagrada, natjecanju ili sličnoj promociji, možemo koristiti podatke koje nam dostavite za upravljanje takvim programima.

Otkrivanje informacija trećim stranama

Podatke koje smo dobili od vas ne otkrivamo trećim stranama.

Iznimke:

• Ako je potrebno - u skladu sa zakonom, sudskim postupkom, u sudskom postupku i/ili na temelju javnih zahtjeva ili zahtjeva državnih tijela na području Ruske Federacije - za otkrivanje Vaših osobnih podataka. Također možemo otkriti podatke o vama ako utvrdimo da je takvo otkrivanje potrebno ili prikladno za sigurnosne svrhe, provedbu zakona ili druge svrhe od javnog značaja.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti osobne podatke koje prikupimo primjenjivoj trećoj strani nasljedniku.

Zaštita osobnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - kako bismo zaštitili vaše osobne podatke od gubitka, krađe i zlouporabe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.

Poštivanje vaše privatnosti na razini tvrtke

Kako bismo osigurali sigurnost vaših osobnih podataka, našim zaposlenicima priopćavamo standarde privatnosti i sigurnosti i strogo provodimo prakse privatnosti.

log a r b r =log a b ili log a b= log a r b r

Vrijednost logaritma se neće promijeniti ako se baza logaritma i broj ispod znaka logaritma podignu na istu potenciju.

Pod znakom logaritma mogu biti samo pozitivni brojevi, a baza logaritma nije jednaka jedinici.

Primjeri.

1) Usporedite log 3 9 i log 9 81.

log 3 9=2, jer je 3 2 =9;

log 9 81=2, jer je 9 2 =81.

Dakle, log 3 9=log 9 81.

Imajte na umu da je baza drugog logaritma jednaka kvadratu baze prvog logaritma: 9=3 2, a broj pod predznakom drugog logaritma jednak je kvadratu broja pod predznakom prvog. logaritam: 81=9 2. Ispada da su i broj i baza prvog logaritma log 3 9 podignuti na drugu potenciju, a vrijednost logaritma se nije promijenila od ovoga:

Dalje, od vađenja korijena n stupnja iz red A je podizanje broja A do stupnja ( 1/n), tada iz log 9 81 možete dobiti log 3 9 uzimanjem kvadratnog korijena broja i baze logaritma:

2) Provjerite jednakost: log 4 25=log 0,5 0,2.

Pogledajmo prvi logaritam. Vađenje kvadratnog korijena iz baze 4 i iz među 25 ; dobivamo: log 4 25=log 2 5.

Pogledajmo drugi logaritam. Baza logaritma: 0,5= 1 / 2. Broj pod znakom ovog logaritma: 0,2= 1/5. Podignimo svaki od ovih brojeva na minus prvu potenciju:

0,5 -1 =(1 / 2) -1 =2;

0,2 -1 =(1 / 5) -1 =5.

Dakle, log 0,5 0,2=log 2 5. Zaključak: ova jednakost je istinita.

Riješite jednadžbu:

log 4 x 4 +log 16 81=log 2 (5x+2). Skratimo logaritme slijeva na bazu 2 .

log 2 x 2 +log 2 3=log 2 (5x+2). Izvadite kvadratni korijen broja i bazu prvog logaritma. Izdvoj četvrti korijen broja i bazu drugog logaritma.

log 2 (3x 2)=log 2 (5x+2). Pretvorite zbroj logaritama u logaritam umnoška.

3x 2 =5x+2. Primljeno nakon potenciranja.

3x 2 -5x-2=0. Kvadratnu jednadžbu rješavamo koristeći opću formulu za potpunu kvadratnu jednadžbu:

a=3, b=-5, c=-2.

D=b 2 -4ac=(-5) 2 -4∙3∙(-2)=25+24=49=7 2 >0; 2 prava korijena.

Ispitivanje.

x=2.

log 4 2 4 +log 16 81=log 2 (5∙2+2);

log 2 2 2 +log 2 3=log 2 12;

log 2 (4∙3)=log 2 12;

log 2 12=log 2 12;

log a n b=(1/ n)∙ log a b

Logaritam broja b na temelju a n jednak umnošku razlomka 1/ n na logaritam broja b na temelju a.

Pronaći:1) 21log 8 3+40log 25 2; 2) 30log 32 3∙log 125 2 , ako se zna da log 2 3=b,log 5 2=c.

Riješenje.

Riješite jednadžbe:

1) log 2 x+log 4 x+log 16 x=5,25.

Riješenje.

Svedimo ove logaritme na bazu 2. Primijenimo formulu: log a n b=(1/ n)∙ log a b

log 2 x+(½) log 2 x+(¼) log 2 x=5,25;

log 2 x+0.5log 2 x+0.25log 2 x=5.25. Evo sličnih pojmova:

(1+0,5+0,25) log 2 x=5,25;

1,75 log 2 x=5,25 |:1,75

log 2 x=3. Prema definiciji logaritma:

2) 0,5log 4 (x-2)+log 16 (x-3)=0,25.

Riješenje. Pretvorimo logaritam na bazi 16 u bazu 4.

0,5log 4 (x-2)+0,5log 4 (x-3)=0,25 |:0,5

log 4 (x-2)+log 4 (x-3)=0,5. Pretvorimo zbroj logaritama u logaritam umnoška.

log 4 ((x-2)(x-3))=0,5;

log 4 (x 2 -2x-3x+6)=0,5;

log 4 (x 2 -5x+6)=0,5. Prema definiciji logaritma:

x 2 -5x+4=0. Prema Vietinom teoremu:

x 1 =1; x 2 =4. Prva vrijednost od x neće raditi, budući da pri x = 1 logaritmi ove jednakosti ne postoje, jer Pod predznakom logaritma mogu biti samo pozitivni brojevi.

Provjerimo ovu jednadžbu na x=4.

Ispitivanje.

0,5log 4 (4-2)+log 16 (4-3)=0,25

0,5log 4 2+log 16 1=0,25

0,5∙0,5+0=0,25

log a b=log c b/log c a

Logaritam broja b na temelju A jednak logaritmu broja b na novoj osnovi S, podijeljeno s logaritmom stare baze A na novoj osnovi S.

Primjeri:

1) log 2 3=lg3/lg2;

2) log 8 7=ln7/ln8.

Izračunati:

1) dnevnik 5 7, ako se zna da lg7≈0,8451; lg5≈0,6990.

c b / log c a.

log 5 7=log7/log5≈0,8451:0,6990≈1,2090.

Odgovor: dnevnik 5 7≈1,209 0≈1,209 .

2) trupac 5 7 , ako se zna da ln7≈1,9459; U5≈1,6094.

Riješenje. Primijenite formulu: log a b =log c b / log c a.

log 5 7=ln7/ln5≈1,9459:1,6094≈1,2091.

Odgovor: dnevnik 5 7≈1,209 1≈1,209 .

Nađi x:

1) log 3 x=log 3 4+log 5 6/log 5 3+log 7 8/log 7 3.

Koristimo formulu: log c b / log c a = log a b . Dobivamo:

log 3 x=log 3 4+log 3 6+log 3 8;

log 3 x=log 3 (4∙6∙8);

log 3 x=log 3 192;

x=192 .

2) log 7 x=lg143-log 6 11/log 6 10-log 5 13/log 5 10.

Koristimo formulu: log c b / log c a = log a b . Dobivamo:

log 7 x=lg143-lg11-lg13;

log 7 x=lg143- (lg11+lg13);

log 7 x=lg143-lg (11∙13);

log 7 x=lg143-lg143;

x=1.

Stranica 1 od 1 1